머신러닝에서 로지스틱 회귀란 샘플이 특정 클래스에 속할 확률을 추정하는 데 널리 사용됩니다
이진 분류기는 추정 확률이 50%가 넘으면 모델은 해당 샘플을 True 50%를 넘지 못하면 False 로 만듭니다.
로지스틱 회귀을 사용하는 목적
로지스틱 회귀의 주된 목적은 이진 분류입니다. 예를들어 이메일이 스팸인지 아닌지, 환자가 특정 질병에 걸릴 확률이 있는지 등을 예측할 수 있습니다.
이때 알 수 있는 것은 로지스틱 회귀는 회귀 알고리즘이만 분류에서도 회귀 알고리즘을 사용할 수 있다는 것을 알 수 있습니다.
로지스틱 함수란
로지스틱 회귀는 로지스틱 함수(또는 시그모이드 함수)를 사용하여 입력값을 0과 1 사이의 확률로 변환합니다.
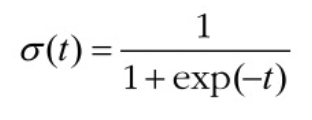
다음은 t의 값에 따라서 데이터가 해당 클래스에 속할 확률을 나타내는 그래프입니다.
로지스틱 회귀 모델이 샘플 t가 양성 클래스에 속할 확률을 추정하면 이에 대한 예측값 y^을 쉽게 구할 수 있습니다.
- 로지스틱 함수로 구한 값이 0.5보다 작으면 0, 0.5보다 크면 1

만약 특정 데이터셋을 입력셋으로 해당 값이 이메일인지 스팸인지 맞추고 싶어 로지스틱 함수를 사용한다면 위에 그림을 예를들어 값이 만약 -2.5 라고 가정했을 때 0.1 정도의 확률이 나온다고 할 수 있겠습니다. 즉 입력 데이터셋으로 0과 1 사이의 확률로 반환하여 회귀지만 이진 분류의 역할을 할 수 있게 합니다.
예를들어 특정 데이터를 입력값으로 넣어 예측 확률이 0.7이면 해당 클래스에 속한다고 판단할 수 있습니다.
로지스틱 회귀 모델의 확률 추정
로지스틱 회귀 모델은 선형 회귀처럼 바로 결과를 내지 않고 '결과값의 로지스틱'을 출력합니다.
다시 말해 선형 회귀는 y를 가지고 비용함수를 게산했다면 로지스틱 회귀 모델은 아닙니다.
대신 예측값을 바로 내지 않고 0과 1사이의 값으로 만드는 로지스틱 함수를 사용하여 0과 1 사이의 확률을 나타냅니다.
로지스틱 회귀 모델 학습과 비용 함수
로지스틱 회귀를 사용했을 때 한 훈련 샘플에 대한 비용 함수는 다음과 같습니다.

- 모델이 양성 샘플 (y = 1)에 대해 0에 가까운 확률을 예측하면 비용이 크게 증가
- 모델이 양성 샘플 (y = 1)에 대해 1에 가까운 확률을 예측하면 비용이 0에 접근
- 모델이 양성 샘플 (y = 0)에 대해 1에 가까운 확률을 예측하면 비용이 크게 증가
- 모델이 양성 샘플 (y = 0)에 대해 0에 가까운 확률을 예측하면 비용이 0에 접근
결정 경계
로지스틱 회귀를 설명하기 위해 붓꽃 데이터셋을 사합니다. 이 데이터셋은 세 개의 품종에 속하는 붓꽃 150개의 꽃잎과 꽃받침의 너비와 길이를 담고 있습니다.
꽃잎의 너비를 기반으로 Iris-Versicolor 종을 감지하는 분류기를 만들면서 로지스틱 회귀를 설명하겠습니다.
다음은 데이터셋을 가져오는 코드입니다.
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
list(iris)
다음으로 로지스틱 회귀 모델을 훈련시킵니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
X = iris.data[["petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)
꽃잎의 너비가 0~3cm 인 꽃에 대해 모델의 추정 확률은 다음과 같습니다.

다음과 같은 특징을 분석할 수 있습니다.
- Iris-Verginica의 꽃잎 너비는 1.4~2.5cm에 분포합니다
- Iris-Verginica가 아닌 꽃잎 너비는 0.1~1.8cm에 분포합니다.
- 꽃잎 너비가 2cm 이상인 꽃은 분류기가 Iris-Verginica라고 강하게 확신합니다.
- 꽃잎 너비가 1cm 아래인 꽃은 분류기가 Iris-Verginica 아니라고 강하게 확신합니다.
양쪽의 확률이 똑같이 50%가 되는 1.6 근방에서 결정 경계가 만들어집니다. 1.6cm보다 크면 분류기는 Iris-Verginica로 분류하고, 그보다 작으면 아니라고 예측할 것입니다. (아주 확실하지 않더라도)
log_reg.predict([[1.7], [1.5]])
# array([1, 0])
이번에는 같은 데이터셋으로 꽃잎의 너비와 꽃잎 길이 두 개의 특성으로 결정경계를 다음과 같이 확인할 수 있습니다.
색깔별로 각각 Iris-Verginica 인 확률을 나타내며 우측은 True 좌측은 False를 나타냅니다.

정리
이렇게 로지스틱 회귀가 어떻게 동작하는지 알아보았습니다. 정리하면 다음과 같습니다
로지스틱 회귀란?
-> 로지스틱 함수를 사용하여 회귀 문제를 이진 분류로 해결할 수 있다
로지스틱 함수란?
-> 입력셋에 대해 0~1 사이의 확률 값으로 만들어주는 함수
결정 경계
-> 로지스틱 함수로 구한 확률 값을 사용하여 True 인지 False 인지 결정하는 경계
로지스틱 회귀를 이용한 값 예측
-> 로지스틱 함수로 결정 경계를 만들어 해당 경곗값을 기준으로 데이터셋의 True 또는 False 를 예측합니다
'AI > Machine Learning' 카테고리의 다른 글
| 머신러닝 - 서포트 백터 머신 (0) | 2024.08.19 |
|---|---|
| 머신러닝 - 모델 훈련, 선형회귀, 경사하강법 (0) | 2024.08.14 |
| 사이킷런 scikit-learn 이란? (0) | 2024.07.09 |
| 여러 개의 레이블을 갖는 하나의 데이터 분류하기 - 다중 레이블 분류 (2) | 2024.07.08 |
| 머신러닝 분류 (숫자 예측) (0) | 2024.07.07 |
