실제 데이터로 작업하기
머신러닝을 배울 때는 인공적으로 만들어진 데이터셋이 아닌 실제 데이터로 실험해보는 것이 가장 좋습니다.
현재 여러 분야에 걸쳐 공개된 데이터셋이 아주 많이 존재합니다. 다음은 데이터를 구하기 좋은 곳입니다.
- 유명한 공개 데이터 저장소
- UC 얼바인 머신러닝 저장소 (http://archive.ics.uci.edu/ml)
- 캐글 데이터셋 (http://www.kaggle.com/datasets)
- 아마존 AWS 데이터셋(https://registry.opendata.aws) - 메타 포털(공개 데이터 저장소가 나열되어 있습니다)
- 데이터 포털 (http://dataportals.org)
- 오픈 데이터 모니터 (http://opendatamonitor.eu)
- 퀸들 (http://quandl.com) - 인기 있는 공개 데이터 저장소가 나열되어 있는 다른 페이지
- 위키백과 머신러닝 데이터셋 목록 (https://goo.gl/SJHN2K)
- Quora.com (https://homl.info/10)
- 데이터셋 서브레딧 (http://www.reddit.com/r/datasets)
캘리포니아 주택 가격 예측 프로젝트
이번 포스팅에서는 캘리포니아 주택 가격 데이터셋을 사용할 것입니다. (데이터셋 다운받기)
캘리포니아 주택 집값을 예측할 수 있는 프로젝트를 진행한다고 가정을 해봅니다.
부동산 회사에 고용된 데이터 과학자로서 할 일은?
- 캘리포니아 인구조사 데이터를 사용하여 캘리포니아 주택 가격 모델 생성을 합니다
- 생성한 모델한테 새로운 측정 데이터를 주었을 때, 해당 구역의 중간 주택 가격을 예측할 수 있게 만들어야 합니다
- 데이터셋에 대한 분석이 필요합니다.
- 캘리포니아의 블록그룹마다 인구, 중간 소득, 중간 주택 가격, 위도, 경도 등 여러 특성들이 존재하고 있습니다.
블록그룹이란 미국 인구조사국에서 샘플 데이터를 발표하는데 사용하는 최소한의 지리적 단위(하나의 블록은 보통 600~3000명 포함)
- 무엇보다 프로젝트를 진행하기 전에 주택 모델 생성의 최종 목적이 무엇인가를 파악하는 것이 매우 중요합니다.
✓ 알고리즘 선택, 모델 평가를 위한 성능 지표 선택, 모델 조정 (tweaking)을 위한 시간 투자 등 결정 요소
문제 정의
- 작업 목적에 맞게 ML 시스템을 설계해야 합니다 -> 집값을 예측하기 위해서는 어떤 학습을 통해 모델을 만들어야 할까?
Q: 지도, 비지도, 준지도, 강화 학습?
✓ A: 레이블 된 훈련 샘플 (각 구역 별 중간 주택 가격이 제시됩니다) -> 지도 학습
Q: 분류 작업, 회귀 작업?, 지도 학습에서 어떤 알고리즘을 사용해야 할까?
✓ A: 주어진 구역의 중간 주택 가격을 예측 -> 회귀 작업
Q: 배치 학습, 온라인 학습?
✓ A: 빠르게 변하는 데이터에 적응 하지 않음 -> 배치 학습 (오프라인 학습)
성능 측정 지표 선택
- 모델 학습을 위한 성능 측정 지표 선택
✓ (학습하는 동안) 모델의 예측 결과에 얼마만큼의 오차가 있는가?
✓ 예로서, 모델이 예측한 주택 값과 레이블로 주어진 실제 값 사이에 오차가 커질 수록 예측에 얼마나 오류가 있는지 확인가능 - RMSE (root mean square error, 평균 제곱근 오차)
✓ 회귀 (regression) 문제에서 사용하는 전형적인 성능 지표입니다
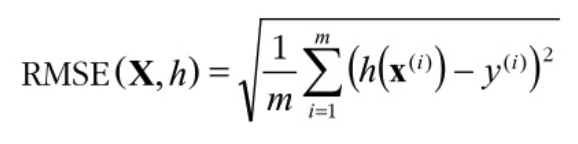
RMSE (Root Mean Square Error) 란
Error(에러) 값에 (Square)제곱을 한 후 Mean(평균) 값을 구한 다음 Root(제곱근)을 씌우는 것입니다.
RMSE는 평균 제곱근 오차라고 불리며 실제 값과 예측 값의 오차를 나타내는 정도입니다. 즉 예측에 오류가 얼마나 많이 있는지를 가늠하게 해줍니다. 물론 값이 작으면 작을수록 좋습니다.
RMSE에서 수식을 분석해보겠습니다.
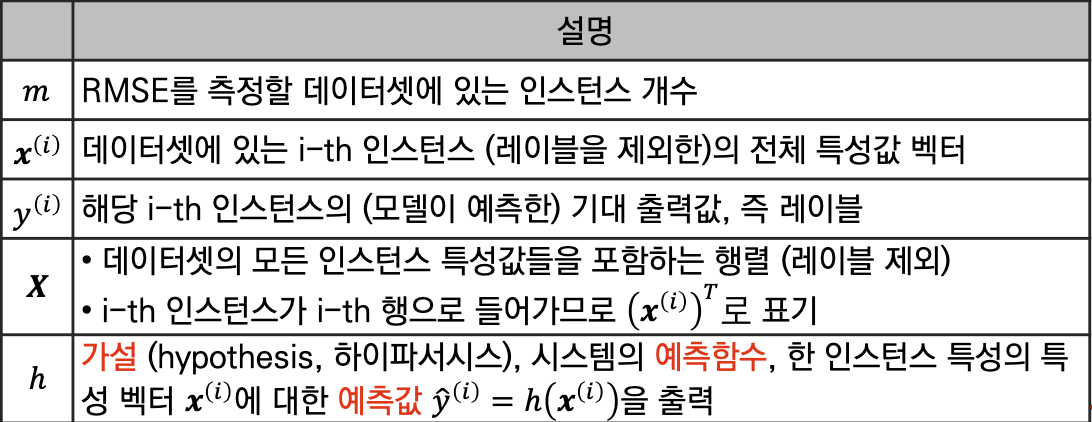
- m: 인스턴스의 수 (행), ex. 인스턴스1: (경도, 위도, 거주자수, 중간 소득, •••)
- x(i): i 번째 인스턴스의 전체 특성값 벡터
- y(i): i 번째 인스턴스의 기계가 예측한 전체 특성값 벡터
- X: RMSE(X,h)에서 X는 데이터셋의 모든 인스턴스 특성값들을 포함하는 행렬(레이블 제외)
- h: 가설, 즉 기계가 백터 값으로 예측값을 출력할 수 있도록 만드는 예측 함수
- 만약 h(x(1)) = (-118.29, 33.91, 1,416, 38,372 •••) 이면 h(예측 함수)로 값을 계산(예측)을 합니다 (158,400)
- 마지막으로 수식의 1부터 m까지의 값을 모두 (h(x(i) - y(i))^2의 구해 평균을 구하면 평균 제곱근 오차 값을 구할 수 있게 됩니다.
데이터 준비하기
데이터를 학습하고 예측하기 위해서는 아나콘다 쥬피터 노트북 또는 VScode처럼 작업할 수 있는 환경이 필요로 합니다.
데이터 가져오기
1. 기본 설정 후 학습할 데이터와 학습한 데이터를 기반으로 테스트할 데이터를 가져옵니다.
import os #Python의 내장 모듈 중 하나로, 파일 및 디렉터리 관리를 위한 함수와 클래스를 제공합니다.
import tarfile #Python의 내장 모듈 중 하나로, tar 파일을 조작하기 위한 함수와 클래스를 제공합니다.
import urllib.request #URL을 통해 데이터를 다운로드하기 위한 모듈입니다.
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/" #데이터를 다운로드할 기본 URL을 지정합니다
HOUSING_PATH = os.path.join("datasets", "housing") #데이터를 저장할 로컬 디렉터리 경로를 설정합니다
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz" #다운로드할 데이터 파일의 URL을 설정합니다
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH): #데이터를 다운로드하고 압축을 해제하는 함수
if not os.path.isdir(housing_path): #가능하지 않은 디렉터리위치라면
os.makedirs(housing_path) #디렉터리를 만든다.
tgz_path = os.path.join(housing_path, "housing.tgz") #다운로드한 파일을 저장할 경로와 저장할 파일이름 지정
urllib.request.urlretrieve(housing_url, tgz_path) #지정된 URL에서 데이터 파일을 다운로드 후 tgz_path 경로에 저장
housing_tgz = tarfile.open(tgz_path) #다운로드한 tar 파일 열기
housing_tgz.extractall(path=housing_path) #tar 파일을 압축 해제 후 압축 해제된 파일들을 housing_path 디렉터리에 저장
housing_tgz.close() #tar 파일 닫기fetch_housing_data()
가져온 데이터 저장하고 읽어오기
fetch_housing_data 메서드를 사용하여 가져온 csv 파일을 가져오는 메서드를 만듭니다.
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv") #housing_path 경로에 housing.csv를 추가
return pd.read_csv(csv_path) #지정한 디렉터리 위치에 있는 housing.csv 파일읽기
데이터가 어떻게 되어 있는지 확인하기
데이터를 housing 변수로 담아낸 후 head 메서드를 사용하여 최초 5개의 행을 출력합니다.
housing = load_housing_data() #함수를 호출하여 데이터셋을 로드하고, 그 결과를 housing 변수에 저장합니다. 이렇게 하면 데이터셋이 메모리에 로드되고 데이터프레임 형태로 저장됩니다.
housing.head() #데이터프레임의 처음 다섯 개의 행을 출력
#head() 메서드는 데이터프레임의 상위 몇 개의 행을 반환하고,기본적으로 처음 다섯 개의 행을 반환
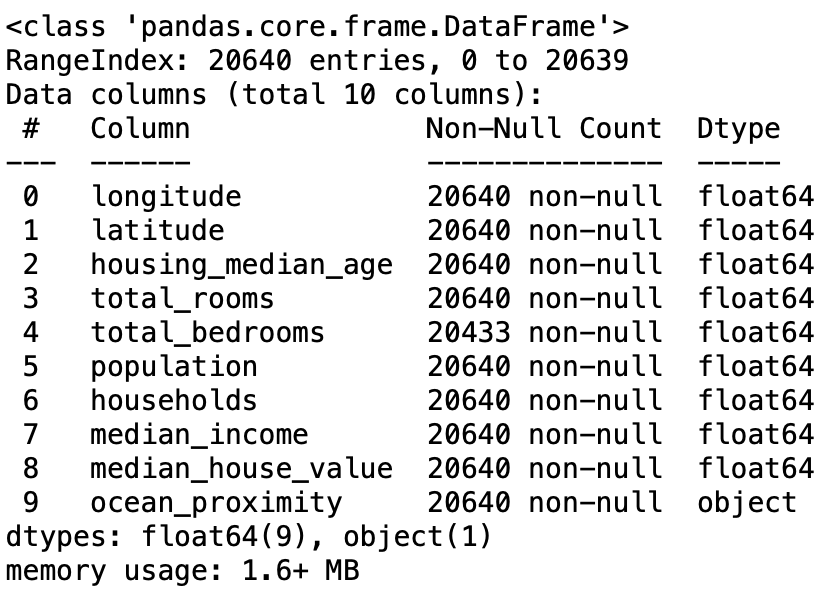
housing.info() #데이터프레임인 housing의 정보를 요약하여 보여주는 메서드
info를 통해 확인해보면 다음과 같이 데이터를 분석할 수 있습니다.
- 데이터셋에 20,640 인스턴스가 있음을 확인할 수 있습니다
- 207개 인스턴스는 total_bedrooms 특성이 없습니다
- ocean_proximity 특성을 제외한 나머지는 모두 숫자형입니다 (float64)
- ocean_proximity 특성은 값이 반복되므로 범주형 특성입니다 (텍스트)
데이터 시각화
데이터를 시각화하여 확인하면 좀 더 직관적으로 분석할 수 있게 됩니다.
시각화를 위해서는 여러 라이브러리가 있으며 다음은 matplotlib를 사용하여 시각화를 한 결과입니다.
import matplotlib.pyplot as plt
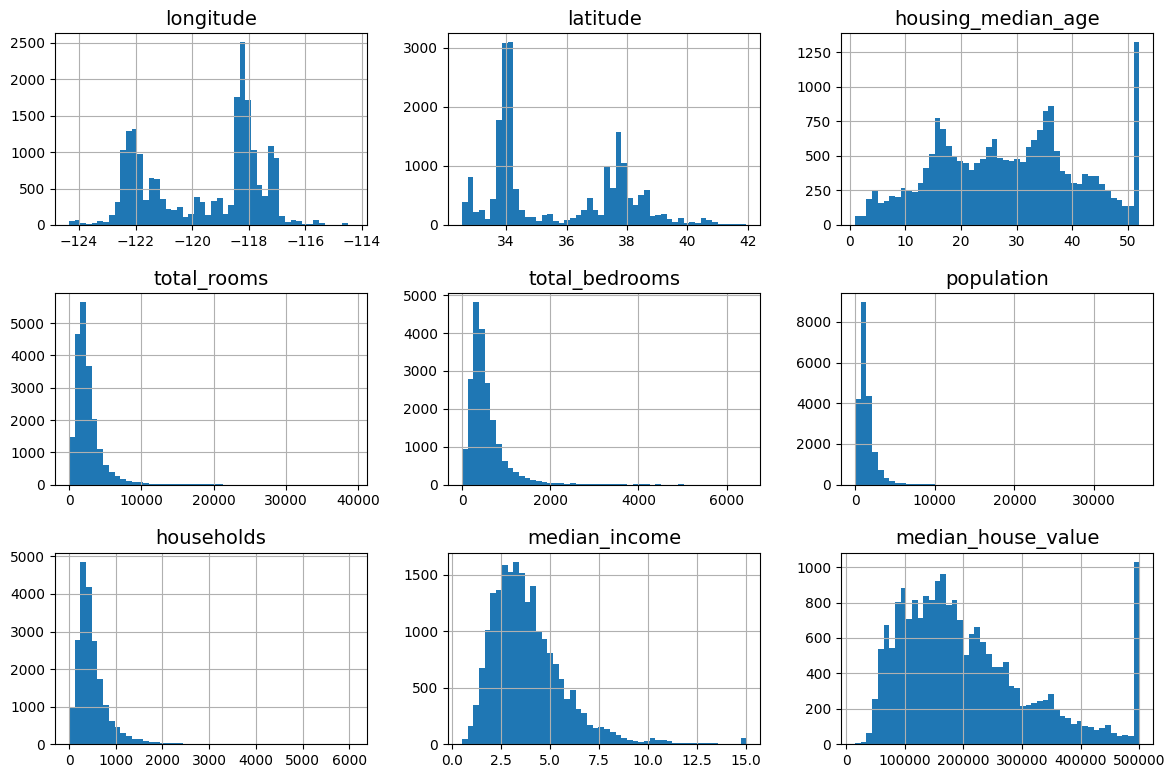
housing.hist(bins=50, figsize=(12, 8))
plt.show()
데이터를 확인했을 때 데이터에 상한 (upper limit)이 있음을 확인할 수 있습니다.
추가로 중간 소득 특성 ($)이 스케일링 되었음을 확인할 수 있습니다. -> 0~50$면..
가져온 데이터 무작위 셔플링
가져온 데이터를 그냥 사용하기보다 무작위로 섞는 과정을 진행합니다. 무작위로 섞어서 훈련셋과 테스트셋을 나눕니다.
np.random.seed(42) #42를 시드로 설정한다, 발생되는 랜덤 값을 예측할 수 있다.
np.random.rand(5) #시드값은 보통 시간 등을 사용해 설정하지만 사람이 수동으로 설정할 수도 있다.import numpy as np
# For illustration only. Sklearn has train_test_split()
def split_train_test(data, test_ratio): #데이터와 테스트셋의 비율을 인자로 받는다.
shuffled_indices = np.random.permutation(len(data)) #데이터 인덱스를 무작위로 섞은 배열을 생성, permutation: 순열, 몇 개를 골라 순서를 고려해 나열한 경우의 수
test_set_size = int(len(data) * test_ratio) #테스트 세트의 크기를 결정
test_indices = shuffled_indices[:test_set_size] #섞인 인덱스 배열에서 처음부터 test_set_size까지의 인덱스를 추출하여 테스트 세트의 인덱스로 설정
train_indices = shuffled_indices[test_set_size:] #테스트 세트로 선택되지 않은 나머지 데이터를 섞어 훈련 세트로 사용하는 것을 의미
return data.iloc[train_indices], data.iloc[test_indices] #함수는 훈련 세트와 테스트 세트를 데이터프레임 형태로 반환
# 무작위로 뽑은 훈련셋,테스트셋
train_set, test_set = split_train_test(housing, 0.2) #테스트셋 비율을 0.2로 설정
len(train_set) #훈련셋의 크기를 확인한다. # 16512
len(test_set) #데이터셋의 크기를 확인한다. # 4128
위에는 무작위로 테스트셋과 훈련셋 나누는 작업을 직접 구현하였지만 sklearn에서는 train_test_split 클래스를 제공합니다.
sklearn 에서 제공하는 train_test_split 을 사용하면 별 다른 구현 없이 데이터를 테스트셋과 훈련셋으로 나눌 수 있습니다.
from sklearn.model_selection import train_test_split
# 난수를 이용하여 랜덤하지 않게 훈련셋과 테스트셋으로 나눈다.
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
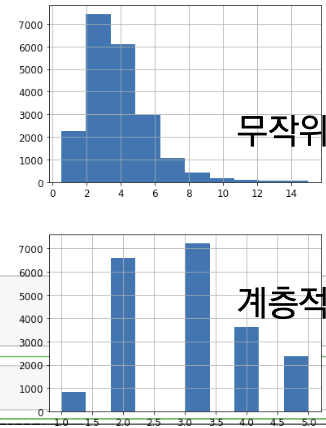
무작위로 샘플링했을 때 발생하는 문제점
위에서 train_test_split 메서드로 무작위로 테스트셋과 훈련셋을 나눴지만 무작위로 나누면 편향될 수 있습니다.
- 만약에 전문가가 중간 소득이 중간 주택 가격을 예측하는데 매우 중요하다고 얘기했다는 가정을 해본다면 이 경우 테스트 셋이 전체 데이터셋에 있는 여러 소득 카테고리를 잘 대표해야 합니다.
- 중간 소득은 수치형 특성이므로 소득에 대한 카테고리 특성을 만들어야 합니다.
- 중간 소득 대부분은 $15,000~$60,000 사이에 모여 있지만 일부는 $60,000를 넘기기도 합니다.
- 계층별로 데이터셋에 충분한 샘플 수가 있어야지 아니면 계층의 중요도를 추정하는데 편향이 발생한다는 것 즉 -> 계층을 너무 많이 나누면 안되고 각 계층이 충분히 커야 합니다(양).
해결 방법 (계층적 샘플링)
위처럼 무작위 샘플링을 통해 편향적인 데이터셋을 만들어내는 것에 해결할 수 있는 방법은 전체 데이터셋에서 무작위로 데이터를 뽑는 것이 아닌 비율에 따라서 뽑는 방법을 사용할 수 있겠습니다. -> 계층적 샘플링이라고 불립니다.
물론 sklearn에서는 이런 작업을 대신 해주는 메서드를 만들었으며 그것이 바로 StratifiedShuffleSplit() 메서드입니다.
# median_income 특성을 이용해서 소득을 나눌 구간(bins)를 설정하고 각 구간에 대응하는 카테고리 레이블을 정의한다.
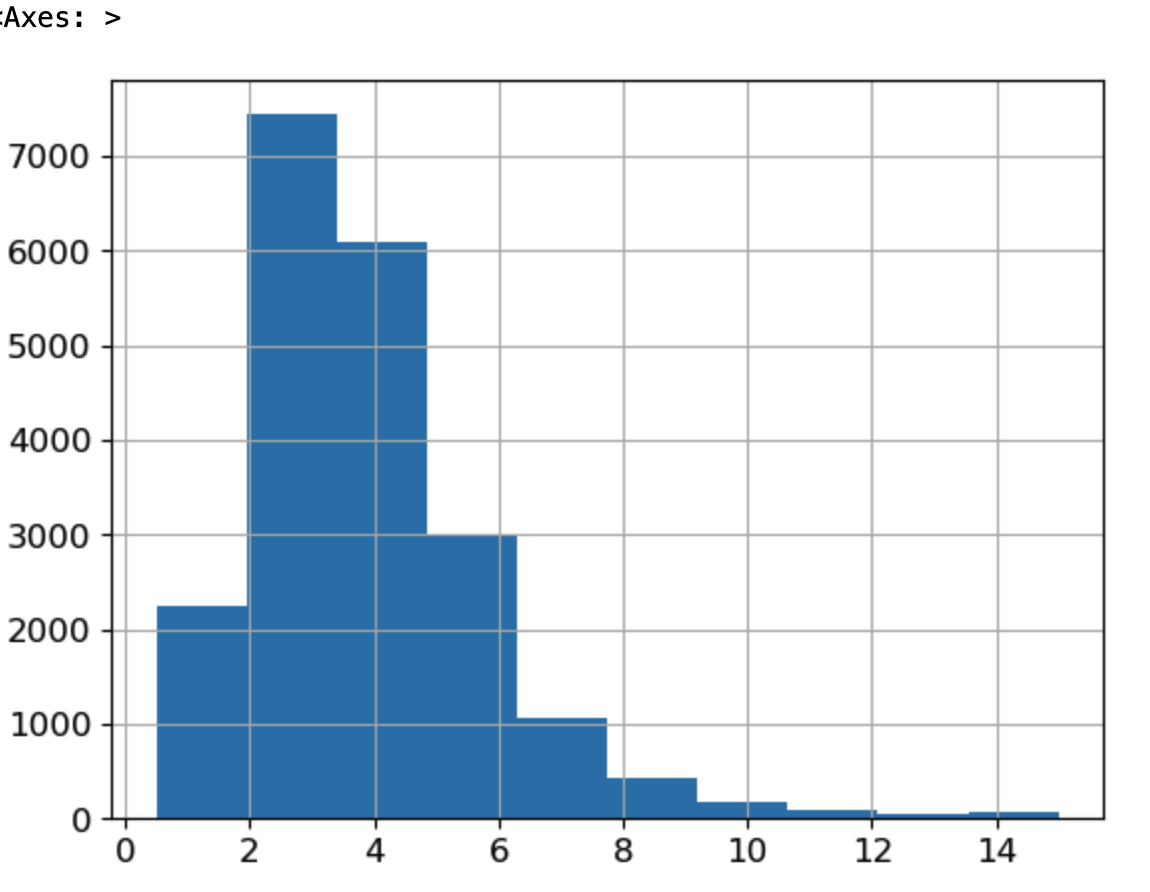
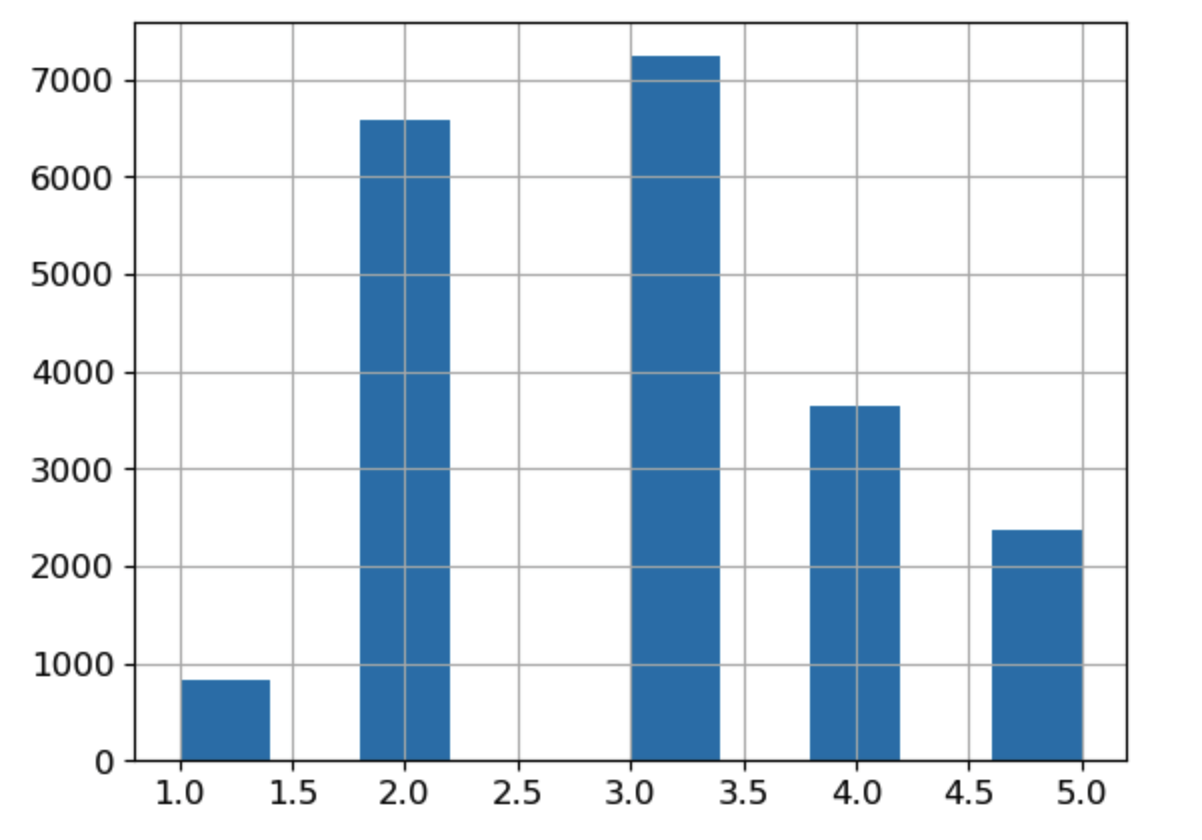
housing["income_cat"] = pd.cut(housing["median_income"], #median_income 열을 기반으로 income_cat 열을 생성한다.
bins=[0., 1.5, 3.0, 4.5, 6., np.inf], #소득을 나눌 구간(카테고리)을 정의, 0에서 1.5, 1.5에서 3.0, 3.0에서 4.5, 4.5에서 6.0 그리고 6.0 이상의 다섯 개의 구간을 설정한다.
labels=[1, 2, 3, 4, 5]) #각 구간에 대응하는 카테고리 레이블을 정의한다. 구간에 따라 소득 카테고리가 1부터 5까지 할당된다.- 먼저 income_cat 이름의 적당한 계층 개수로 특성을 만들었습니다.
- 카테고리를 1, 2, 3, 4, 5로 나누고, 카테고리 1은 0에서 1.5까지 범위(즉$15,000 이하)이고 카테로기 2는 1.5에서 3까지 범위가 되는 식입니다
- 무작위로 막 뽑기에는 2~6 구간이 너무 많아서 그쪽 소득으로 편향될 가능성이 있기 때문에 계층으로 나눠 각 계층에서 일정 몇%씩 뽑는 그런 메커니즘으로 진행하면 공정해집니다.
-> 즉 방금 한 구간나누기는 계층적 샘플링을 하기 위해서 각 값이 본인의 카테고리를 잘 대표할 수 있도록 구간을 나눈 것
이제 위에서 만든 소득 카테고리를 기반으로 계층적샘플링을 할 준비가 끝났습니다.
- 계층적샘플링이란? -> 자신이 속한 구간을 잘 대표하는 데이터들을 편향하지 않게 잘 뽑는 것입니다.
중간소득을 기반으로 만든 카테고리 특성을 sklearn의 StratifiedShuffleSplit을 사용하여 계층 샘플링을 할 차례입니다.
from sklearn.model_selection import StratifiedShuffleSplit #계층적 셈플링
# 데이터를 분할하는 횟수=1, 테스트셋 비율=0.2, 난수 초기값을 설정
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
#위에서 설정한 계층적 샘플링 객체인 split에 split메서드를 사용하여 housing 데이터에서 새로만든 소득 카테고리를 가지고 계층적 샘플링을 한다
for train_index, test_index in split.split(housing, housing["income_cat"]): # housing데이터프레임에서 imcome_cat을 사용하여 분할, split메서드를 호출하여 데이터를 분할한다.
strat_train_set = housing.loc[train_index] #계층적셈플링 훈련셋 ,loc: pandas 라이브러리에서 데이터프레임에서 특정 행을 선택하거나 조건에 맞는 데이터를 인덱싱하는 기술
strat_test_set = housing.loc[test_index] #계층적셈플링 테스트셋
# loc:열만 가져오기, df.loc[칼럼슬라이싱]#이를 통해 전체 데이터셋에서 각 소득 카테고리가 차지하는 비율을 확인할 수 있다.
housing["income_cat"].value_counts() / len(housing) #income_cat열의 각 소득 카테고리별 데이터 포인트 비율을 계산하는 코드다.
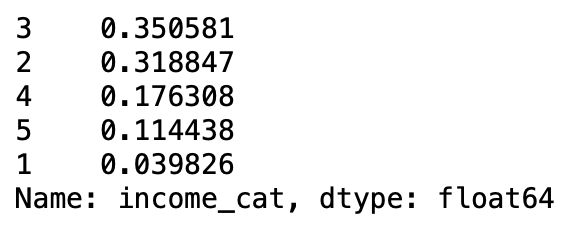
계층적샘플링을 했을때와 무작위로 뽑았을때 나타나는 오류 오차범위를 확인할 수 있습니다.
-> 확인결과 랜덤으로 뽑을때 비율이 방금 계층 샘플링으로 만든 housing["income_cat"]보다 부정확하다는 것을 확인 할 수 있습니다
def income_cat_proportions(data): #소득 카테고리별 데이터 포인트 비율을 계산하는 함수
return data["income_cat"].value_counts() / len(data)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({
"Overall": income_cat_proportions(housing),#각 소득 카테고리별 데이터 포인트 비율얻기
"Stratified": income_cat_proportions(strat_test_set),#각 소득 카테고리별 데이터 포인트 비율얻기
"Random": income_cat_proportions(test_set),#무작위 샘플링으로 생성된 소득 카테고리별 데이터 포인트 비율얻기
}).sort_index() #Overall:전체 데이터셋, Stratified: 테스트셋, Random: 랜덤 테스트셋
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100compare_props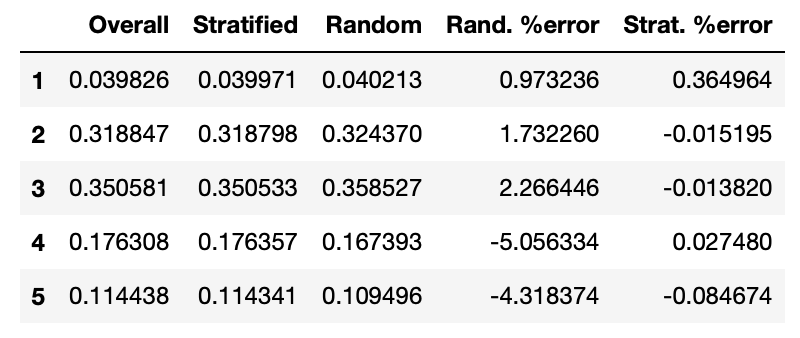


- 계층 샘플링(구간을 나눠)을 사용해 만든 테스트셋의 소득 카테고리 비율이 전체 데이터셋 비율과 가까운 것을 확인할 수 있다.(공평)
계층적 샘플링을 통해서 데이터도 잘 뽑았겠다 이제 사용한 (방금 만들었던) income_cat 열을 지워줍니다.
for set_ in (strat_train_set, strat_test_set):
#axis=0: 행삭제, axis=1: 열삭제
set_.drop("income_cat", axis=1, inplace=True)
계층적 샘플링 후 시각화
계층적샘플링을 통해서 분리한 훈련셋을 이용해 시각화를 합니다.
#복사를 해서 사용하는 이유는 기존 훈련셋을 손상시키지 않기 위해 복사본을 만드는 것이다.
housing = strat_train_set.copy() #계층 샘플링을 사용해 만든 테스트셋, copy()는 값만 복사하는 것, 참조 Xhousing.plot(kind="scatter", x="longitude", y="latitude")
save_fig("bad_visualization_plot") #생성된 시각화를 파일로 저장하기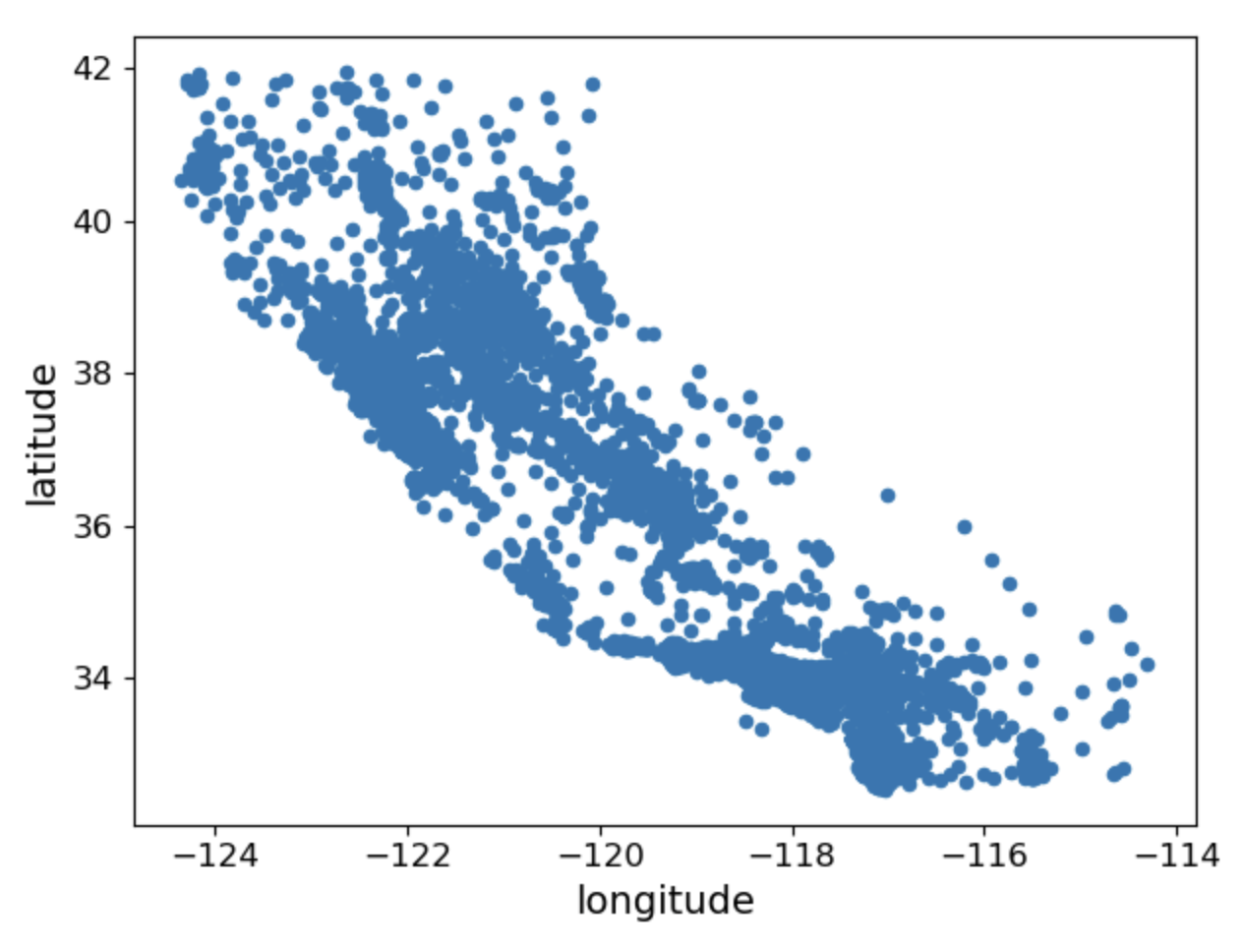
하지만 위는 안좋은 시각화 파일입니다. 좋은 시각화 파일을 만들려면 투명도를 설정해야합니다.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
save_fig("better_visualization_plot")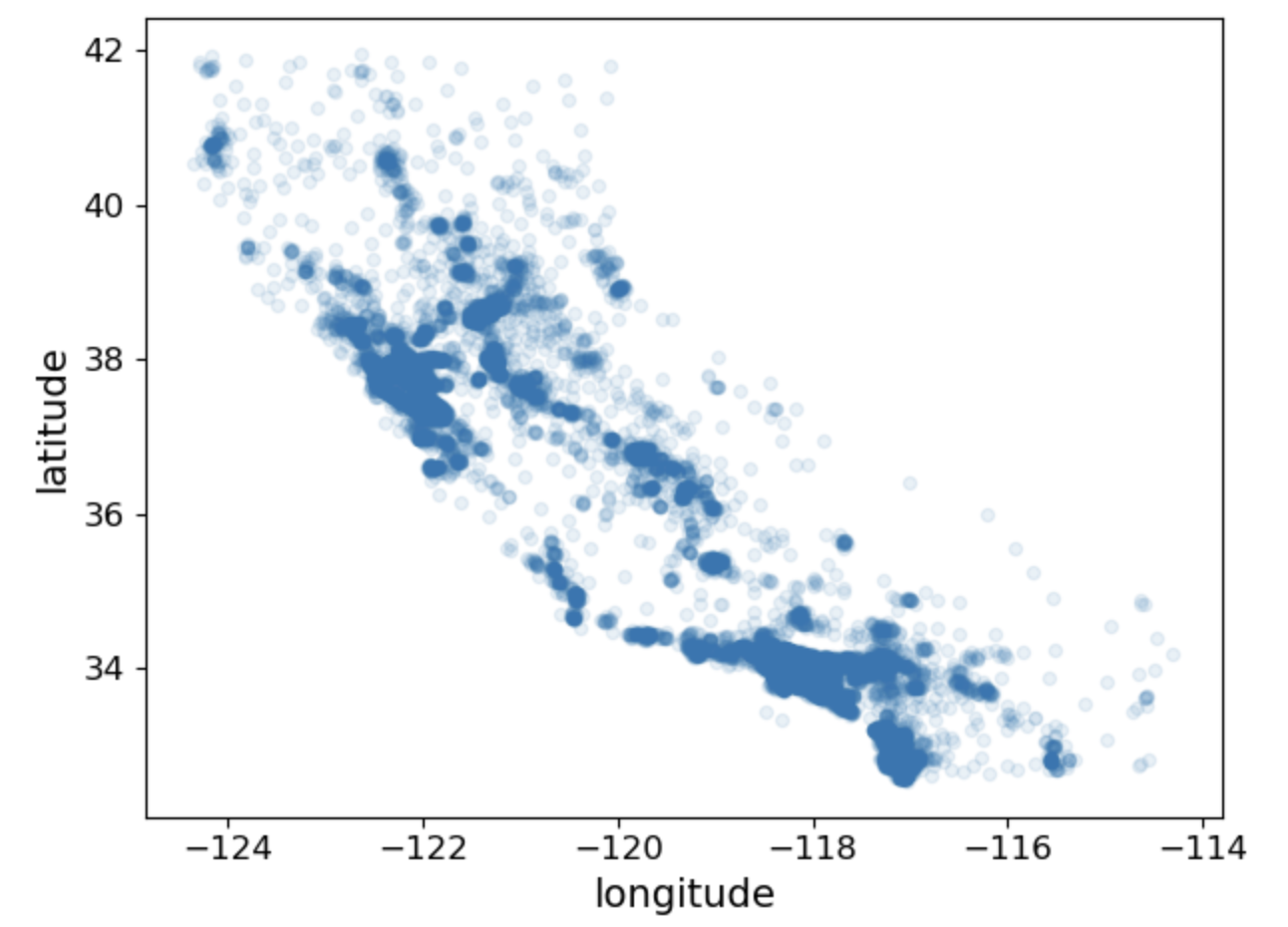
다음처럼 설정하면 그래프 유형, 축 이름, 컬러맵, 투명도 등을 설정하여 데이터 시각화 할 수 있습니다
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()
save_fig("housing_prices_scatterplot")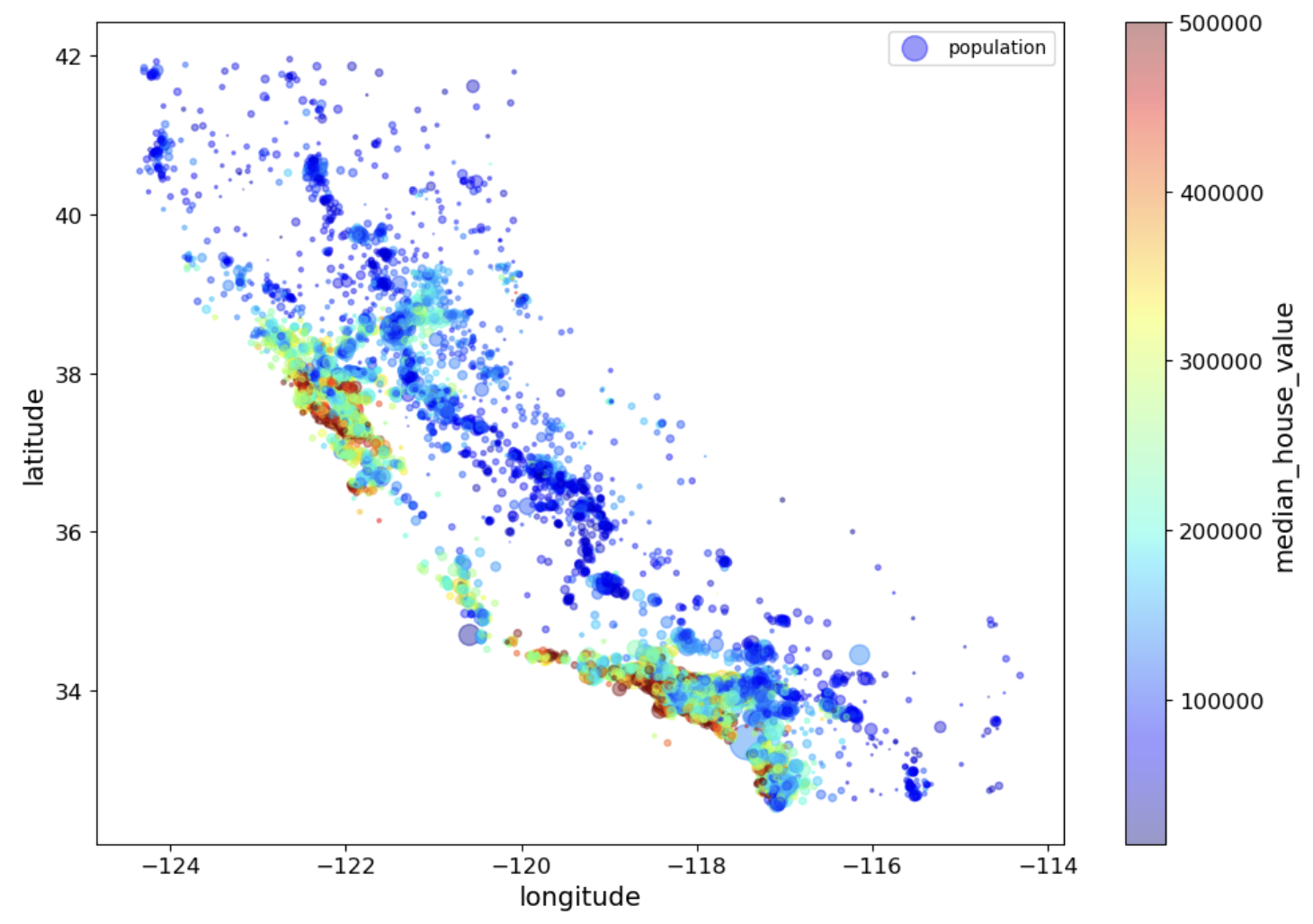
상관관계
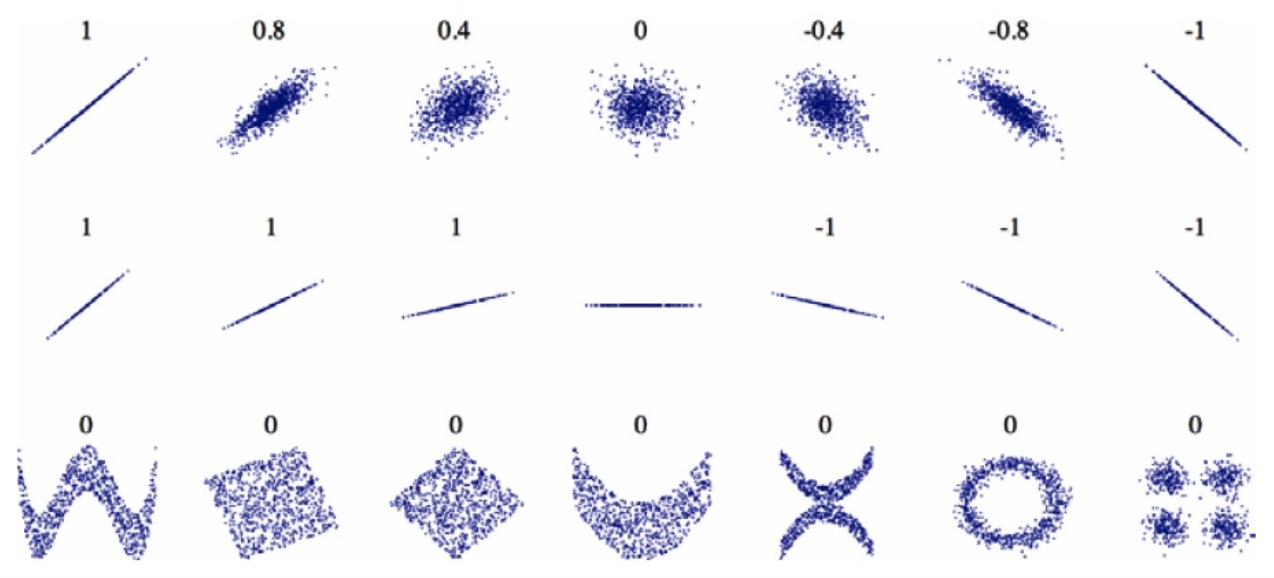
다음으로 상관관계 corr()를 조사해야합니다. 피어슨의 r 이라고 불리는 표준 상관 계수는 -1 < r < 1 의 범위를 갖습니다.
- 1에 가까우면 강한 양의 상관관계 (예: 중간 주택 가격이 상승하면 중간 소득도 증가하는 경향)
- -1에 가까우면 강한 음의 상관관계 (예: 위도가 올라갈 수록 중간 주택 가격은 조금씩 내려가는 경향)
- 특징으로는 상관계수는 선형적인 상관관계만 측정할 수 있으며 비선형적인 상관관계는 측정할 수 없습니다
corr_matrix = housing.corr(numeric_only=True) #각 열(특성) 간의 상관 관계를 계산한다.
corr_matrix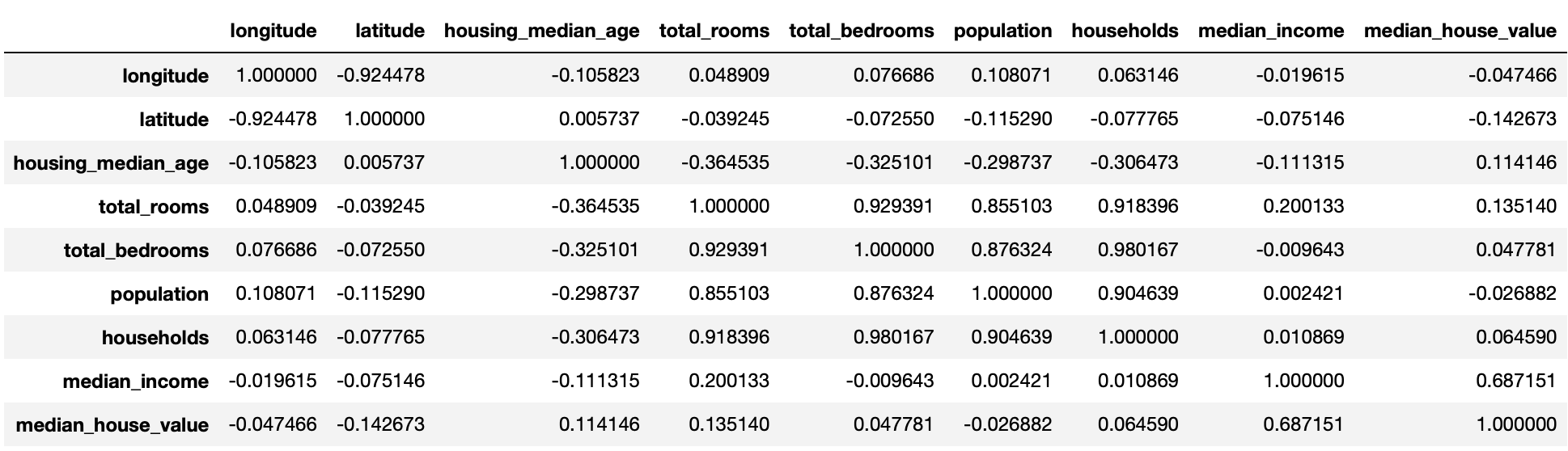
상관관계의 값에 따라 데이터는 여러 형태로 존재할 수 있습니다.
corr_matrix["median_house_value"].sort_values(ascending=False)
#"median_house_value" 열과 다른 모든 열 간의 상관 관계를 가져와 내림차순으로 정렬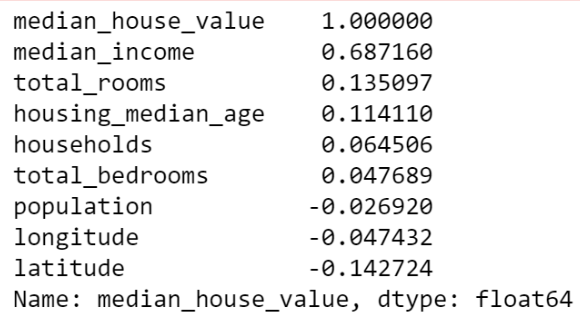
다음은 상관계수를 시각화한 결과입니다.
# from pandas.tools.plotting import scatter_matrix # For older versions of Pandas
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"] # 4x4
scatter_matrix(housing[attributes], figsize=(12, 8))# 선택한 특성 간의 모든 산점도를 생성한다. 그림 크기 설정
save_fig("scatter_matrix_plot")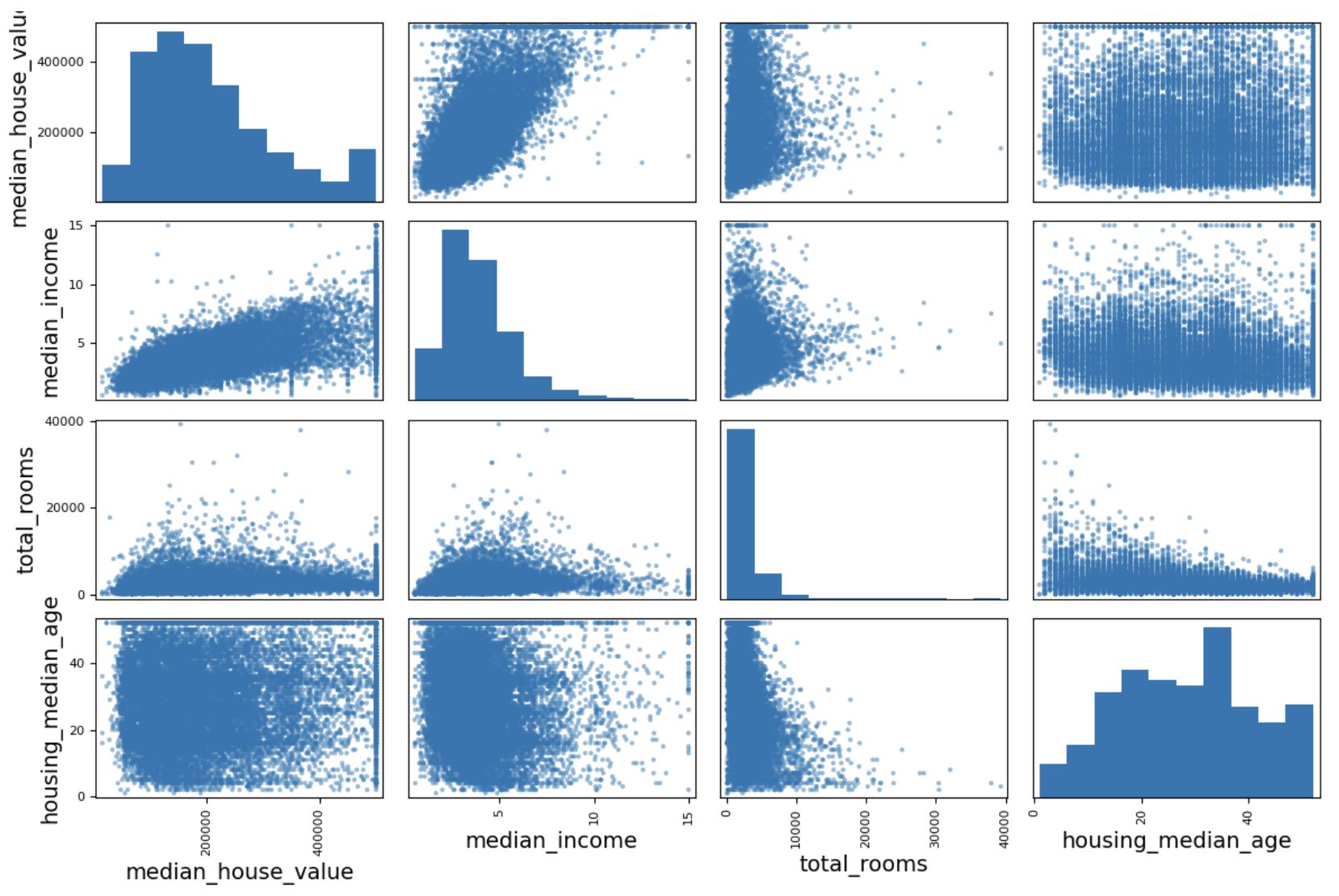
- 중간 주택 가격(median_house_value)을 예측하는데 가장 유용할 것 같은 특성을 중간 소득(median_income)이므로 상관관계 산점도를 확대대하여 분석해봅니다.
✓ 위에서 상관관계는 선형적인 상관관계만 측정할 수 있다고 하였는데 아래에서
housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
plt.axis([0, 16, 0, 550000]) # 가격 제한 50000이나 이상한 데이터를 학습하지 않게 제거작업이 필요할 수 있다.
save_fig("income_vs_house_value_scatterplot")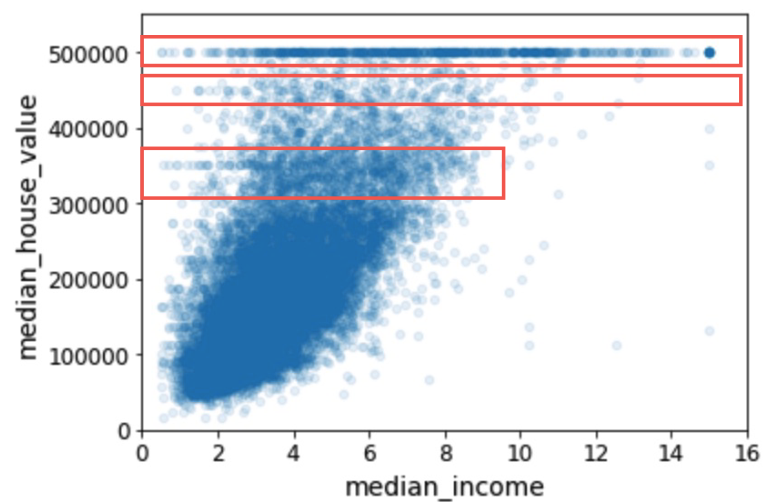
- 상관관계가 매우 강하다는 것을 알 수 있으며
- 1. 위쪽으로 향하는 경향을 볼 수 있고, 포인트들이 너무 널리 퍼져 있지 않음 -> 수직일수록 좋고 주변에 지져분한게 없어야 좋음.
- 2. 앞서 본 가격 제한값이 $500,000에서 수평선을 잘 보임.
이렇게하여 median_income 과 median_house_value 가 집값을 예측하는데 관계가 높음을 알 수 있습니다.
특성 조합하기 (특성공학)
특성을 조합해서 집값을 예측할 수 있는 유의미한 새로운 특성을 만들 수 있습니다.
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]
새로 만든 특성들과 median_house_value (중간 주택 가격)과의 상관관계(피어슨의 r)을 확인해보고 유의미성을 확인합니다.
corr_matrix = housing.corr() # 새로운 조합으로 만들어진 특성간의 상관관계 파악
corr_matrix["median_house_value"].sort_values(ascending=False)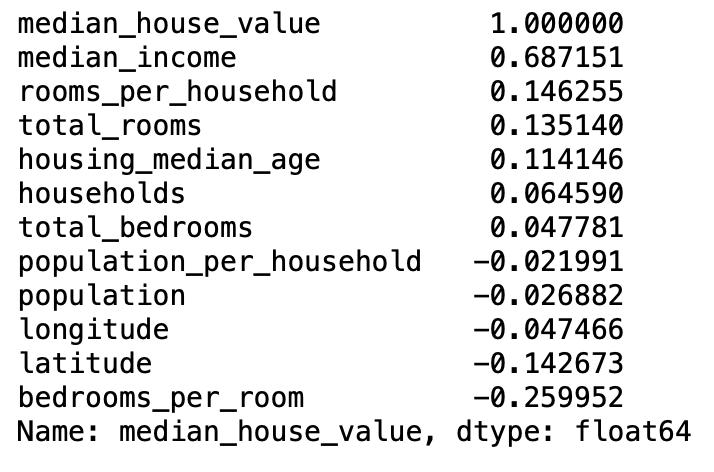
새로 만든 특성들이 추가된 상태에서 새로 상관관계를 출력합니다.
- 새로운 rooms_per_household는 양의 상관관계를 보이고
- 새로운 bedrooms_per_room은 음의 상관관계를 보이고
- 새로운 population_per_household도 음의 상관계수를 보입니다.
이후 새로운 rooms_per_household 특성과 중간 주택 가격의 산점도(시각화)로 상관관계도 파악해볼 수 있습니다.
# 특성을 조합해서 새로운 특성을 가지고 그림그리기
housing.plot(kind="scatter", x="rooms_per_household", y="median_house_value",
alpha=0.2) # x축의 데이터 값을 rooms_per_household, y축의 데이터 값을 median_house_value 값으로 설정
plt.axis([0, 5, 0, 520000])
#x축은 0에서 5까지, y축은 0에서 520,000까지의 범위로 지정합니다. 이렇게 범위를 설정함으로써 산점도의 축의 스케일을 조절할 수 있습니다
plt.show()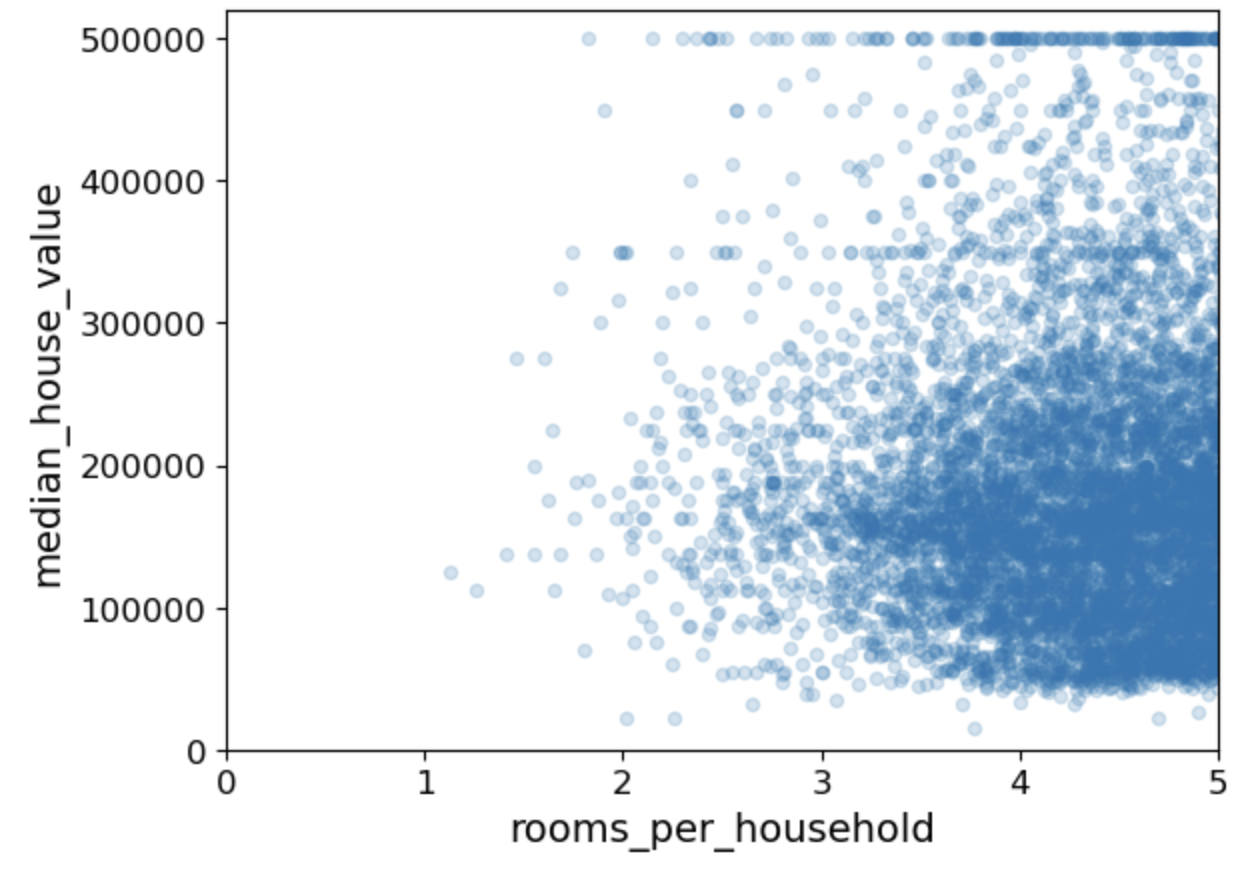
데이터 정제
머신러닝 알고리즘을 위한 데이터를 준비해야하는데 이 작업은 수동으로 하는 대신 함수를 만들어서 자동화를 해야합니다. 이유는
* 어떤 데이터셋에 대해서도 데이터 변화을 손쉽게 반복할 수 있습니다. (다음에 새로운 데이터셋을 사용할 때)
* 향후 프로젝트에 사용할 수 있는 변환 라이브러리를 점진적으로 구축할 수 있습니다.
* 실제 시스템에서 알고리즘에 새 데이터를 주입하기 전에 변환시키는 데 이 함수를 사용할 수 있습니다.
* 여러 가지 데이터 변환을 쉽게 시도해볼 수 있고 어떤 조합이 가장 좋은지 확인하는 데 편리합니다.
다음은 레이블 데이터에 같은 변형을 적용하지 않기 위해 훈련 데이터셋에서 레이블(정답)을 분리해서 따로 저장하는 것입니다
# drop은 지우는 것이 아니라 해당 값만 임시로 뺀다는 것이다, axis=1은 열을 기준으로 삭제하라는 의미
housing = strat_train_set.drop("median_house_value", axis=1)
#데이터프레임에서 median_house_value 열만 선택하여 housing_labels 시리즈에 저장
housing_labels = strat_train_set["median_house_value"].copy()
NULL 값 대응하기
다음으로 housing에서 null 값이 들어있는 행을 나타냅니다.
sample_incomplete_rows = housing[housing.isnull().any(axis=1)].head()
sample_incomplete_rows
비어있는 null값이 들어있는 데이터를 가지고 모델을 훈련하게 될 경우 오류가 날 수 있습니다.
해결할 수 있는 방안에는 다음 3가지가 있습니다.
1. 비어있는 해당 인스턴스를 제거한다.
sample_incomplete_rows.dropna(subset=["total_bedrooms"]) # option 1: 해당 인스턴스 제거 dropna(drop not a number)2. 비어있는 해당 특성을 삭제한다.
sample_incomplete_rows.drop("total_bedrooms", axis=1) # option 2, 해당 특성 제거, total_bedrooms 삭제3. 비어있는 값을 다른 값으로 대체한다(중간값, 평균 등등)
median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True) # option 3: 다른 값으로 채우기, 중간 값으로 채움
SimpleImputer 클래스로 대응하기
비어있는 값을 채우기 위한 sklearn에서 만든 SimpleImputer 클래스가 존재합니다.
● SimpleImputer는 여러 가지 전략을 통해 결측값을 대체할 수 있습니다
- 평균값(mean): 각 열의 평균값으로 결측값을 대체합니다. 수치형 데이터에 적합합니다.
- 중앙값(median): 각 열의 중앙값으로 결측값을 대체합니다. 수치형 데이터에 적합하며, 이상치(outliers)의 영향을 줄일 수 있습니다.
- 최빈값(most_frequent): 각 열의 최빈값으로 결측값을 대체합니다. 수치형 및 범주형 데이터 모두에 적합합니다.
- 상수값(constant): 사용자 정의 상수값으로 결측값을 대체합니다. 특정 값을 지정하여 결측값을 대체하고 싶을 때 사용합니다.
평균값: 1,2,3,4,5 = (1+2+3+4+5) / 5
중앙값: 1,2,3,4,5 = (1+5) / 2
● 집값을 예측하는 현재 데이터에서는 median을 사용하여 중간값으로 채웁니다.
from sklearn.impute import SimpleImputer #데이터셋에 비어있는 특성값을 채우기 위한 변환기
imputer = SimpleImputer(strategy="median") #클래스를 중간값 채우기로 설정
# (strategy="median"은 중간값으로 채운다는것을 의미한다)
● 중간값이 수치형 특성에서만 계산될 수 있기 때문에 텍스트 특성인 ocean_proximity를 제외한 데이터 복사본을 생성합니다. (중요)
housing_num = housing.drop("ocean_proximity", axis=1) # 숫자가 아닌 특성인 ocean_proximity 제거
# alternatively: housing_num = housing.select_dtypes(include=[np.number])
● 원본 데이터에서 housing에서 ocean_proximity 특성을 뺀 나머지 데이터에서 비어있는 값이 있으면 중간값으로 대체합니다.
- fit = 학습
# imputer 객체를 사용하여 housing_num 데이터프레임에서 중간값을 계산한다.
# fit()메서드를 호출하면 imputer객체가 housing_num 데이터프레임에서 각 열의 중간값 계산
imputer.fit(housing_num) # imputer클래스한테 housing_num 데이터의 중간값을 계산하고 비어있는 곳에 채우도록 학습
● 다음 명령어를 수행하면 채워질 각 특성들의 중간값을 확인할 수 있습니다.
- imputer는 각 특성의 중간값을 계산해서 그 결과를 객체의 statistics_ 속성에 저장합니다.
imputer.statistics_ # 중간값 확인 (채워질 값)
● SimpleInputer와 median 함수를 사용하여 결과를 비교하여 같은지 확인할 수도 있습니다.
# SimpleImputer와 직접 median()을 이용해 계산한 결과 비교
housing_num.median().values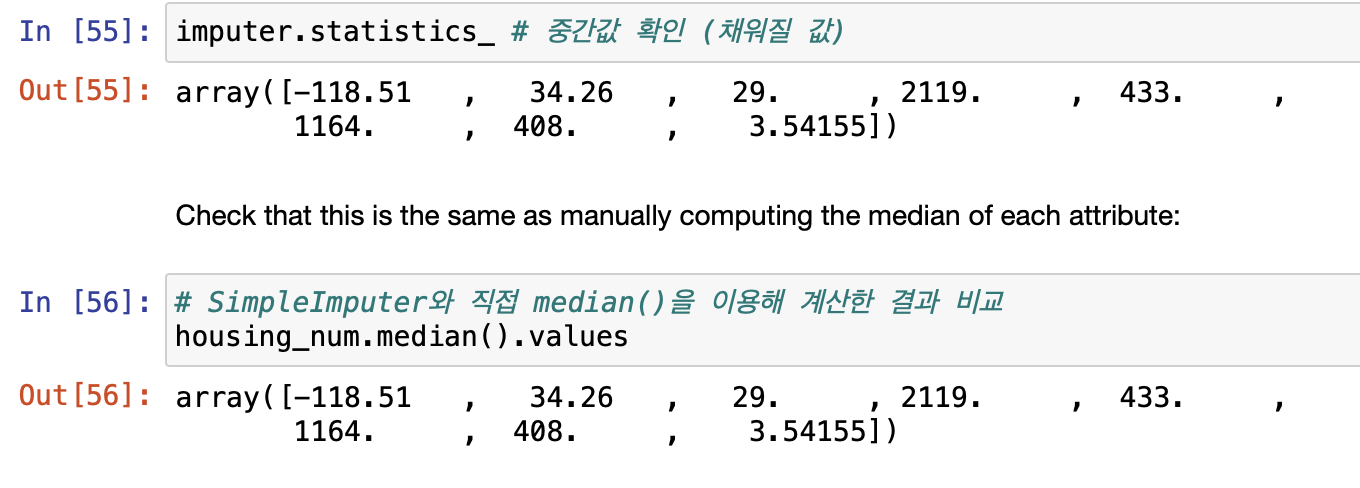
학습된 imputer 객체를 사용해 훈련 세트에서 누락된 값을 학습한 중간값으로 바꿀 수 있습니다.
- fit(학습)된 imputer 객체로 housing_num에 비어있는 값을 transform(변환)시켜준다.
- imputer.fit_transform(housing_num)메서드로 훈련과 변환을 한번에 시킬 수 있다.
# housing_num에서 빠져있던 값들이 imputer에 설정된 중간값으로 채워진다.
X = imputer.transform(housing_num) # 빠져있던 것들이 채워진다.아래는 변형된 특성들이 들어 있는 평범한 numpy 배열이다. 이를 다시 pandas DataFrame으로 되돌린다.
# housing_tr: 새로운 데이터프레임을 저장할 변수
# pd.DataFrame() 생성자를 사용해 새로운 데이터프레임을 만든다
# X = 비어있던 값을 중간값으로 채워넣은 데이터(housing_num)가 들어간다.
# columns: 열 이름을 지정한다. housing_num의 열 이름과 동일하게 설정
# index=housing.index: housing(원본) 인덱스를 그대로 사용해 행 인덱스를 원본과 동일하게 설정
housing_tr = pd.DataFrame(X, columns=housing_num.columns, #훈련셋의 누락된 값을 중간값으로 채우기
index=housing.index) #NumPy 배열을 Pandas DataFrame으로 되돌리기
# 비어있던 특성의 행에 중간값들이 채워진게 보여진다.
housing_tr.loc[sample_incomplete_rows.index.values]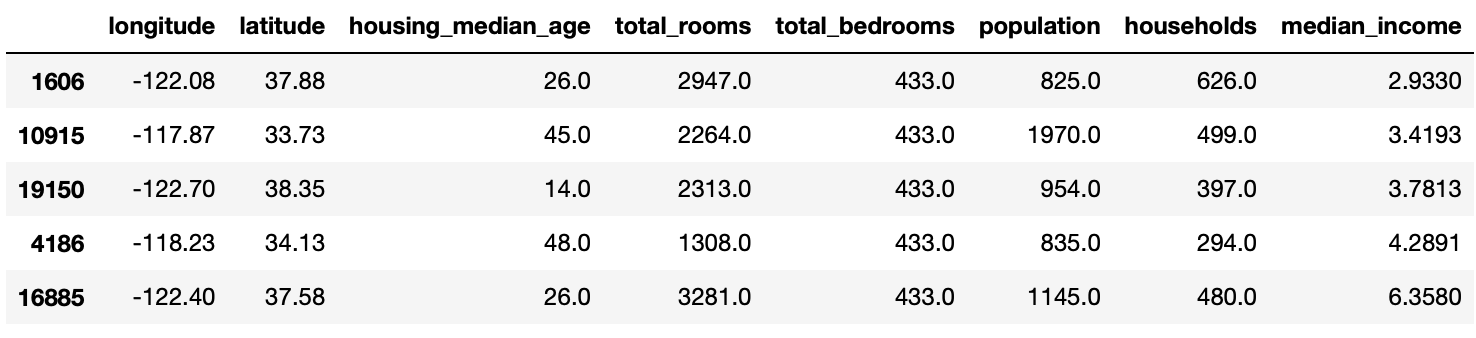
숫자가 아닌 값에 대응하기
추가로 숫자가 아닌 데이터를 처리해야하는 경우가 있을 수 있습니다. housing 데이터에서 범주형특성인 "ocean_proximity" 열 값을 housing_cat에 담습니다.
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
텍스트에서 숫자로 변환하기 (해결방법 X)
범주형 특성은 각 범주에 대응하는 숫자로 변환하되 숫자로만 표현하면 실제 값의 의미하고는 멀어질 수 있는 값이 배정될 수 있습니다.
그러므로 one-hot인코딩(이진특성)을 만들어서 해결할 수 있습니다. 이를 위해 sklearn의 OrdinalEncoder 클래스를 사용합니다.
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder() #각 범주를 대응하는 숫자로 변환
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]
# housing_cat: ocean_proximity의 값을 갖고
# fit_transform(): 학습과 변환을 한 번에 housing_cat을 이용하여 학습과 변환
값은 array([[0.], [0.], [4.], [1.], [0.], [1.], [0.], [1.], [0.], [0.]]) 입니다.
- 하지만 위처럼 값을 표현하면가까이 있는 두 값이 떨어져 있는 두 값보다 유사하다고 판단하는 문제가 발생합니다.
- 예를 들어 0과 4보다 0과 2가 더 가깝습니다 (숫자 상으로는), 그러나 실제로는 4( NEAR OCEAN)이 2(ISLAND)보다 0 (<1H OCEAN)과 유사합니다.
- 정수보다 이진 특성을 만들어서 해결할 수 있습니다 -> one-hot 인코딩
텍스트에서 숫자로 변환하기 (해결방법 O)
sklearn에서 제공하는 one-hot 인코딩을 사용한다면 범주의 값을 원-핫 벡터로 바꾸기 위한 OneHotEncoder 클래스를 제공합니다.
from sklearn.preprocessing import OneHotEncoder
# 두개의 백터의 값을 제곱해서 차를 더하고 제곱근을 씌워준다.
cat_encoder = OneHotEncoder()
# housing_cat = housing[["ocean_proximity"]] 범주형 특성이다.
# fit_transform(): 학습과 변환을 한 번에 housing_cat을 이용하여 학습과 변환
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hothousing_cat_1hot.toarray() # 범주형 특성을 가지고 핫인코딩한 결과
# 밀집 배열을 출력하도록 설정, True면 희소 행열을 출력
# cat_encoder 객체를 사용하여 범주형 데이터인 Housing_cat을 원-핫 인코딩한다.
cat_encoder = OneHotEncoder(sparse_output=False)
# fit_transform 메서드로 housing_cat 데이터프레임의 각 범주형 특성을 원-핫 인코딩하여 수치형 특성으로 변환
# 결과 데이터는 housing_cat_1hot에 저장, fit_transform으로 변환 작업 수행
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
변환기 함수로 만들기
추가로 나만의 변환기를 만들어서 새로운 특성을 만들 수 있습니다.
- init 으로 add_bedrooms_per_room을 True로 만든다면 add_bedrooms_per_room 특성을 생성하는 클래스입니다.
- rooms_per_household (방 수 / 인구수) 특성을 만듭니다
- population_per_household ((방 수 / 인구수) / 방 수) 특성을 만듭니다.
- 이후 새로 bedrooms_per_room 특성을 만들지 말지를 결정하고 새롭게 만든 특성들을 반환합니다
from sklearn.base import BaseEstimator, TransformerMixin
#사용자 정의 변환기를 정의하고 해당 변환기를 사용하여 데이터셋으로 새로운 특성을 만들기
# column index, 데이터셋의 열 인덱스를 나타내는 변수들, 특정 열을 접근할 때 사용
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
# 사용자 정의 변환기를 정의합니다. 이 클래스는 BaseEstimator, TransformerMixin 클래스를 상속받는다.
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
# add_bedrooms_per_room은 나중에 특성을 추가할 때 침실 수 대비 방의 비율을 추가할지 여부를 결정
def __init__(self, add_bedrooms_per_room=True): # no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
# 학습 데이터셋을 입력받아 아무 작업을 수행하지 않고 self를 반환
# 변환기는 아무런 학습을 하지 않기때문에 빈 메서드로 정의
def fit(self, X, y=None):
return self # nothing else to do
# 변환을 수행하는 메서드로, 주어진 데이터셋 X에 대해 새로운 특성을 계산하고 반환
def transform(self, X):
# 가구당 방의 수를 계산한다
# X에서 rooms_ix에 해당하는 열과 Households_ix에 해당하는 열의 값을 나눈다.
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
# 가구당 인구 수를 계산한다. 인구수 / 가구수
# X에서 population_ix에 해당 열과 households_ix에 해당 열의 값을 나눈다.
population_per_household = X[:, population_ix] / X[:, households_ix]
# 매개변수가 True인 경우 침실 수 대비 방의 비율을 계산
if self.add_bedrooms_per_room: #
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
# return np.c_[인자값, 가구당 방의 수, 가구당 인구 수, 방당 침대 수]
# np.c_: 두 개의 1차원 배열을 칼럼으로 세로로 붙여서 2차원 배열 만들기
return np.c_[X, rooms_per_household, population_per_household,
bedrooms_per_room]
else: # 침실 수 대비 방의 비율을 추가하지 않는다.
# np.c_: 두 개의 1차원 배열을 칼럼으로 세로로 붙여서 2차원 배열 만들기
return np.c_[X, rooms_per_household, population_per_household]
# CombinedAttributesAdder클래스의 attr_adder 객체를 만든다.
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
# 위에서 만든 변환기로 housing의 값들로 X(housing.values), rooms_per_household,
# population_per_household 값들을 2차원 배열로 반환한다.
housing_extra_attribs = attr_adder.transform(housing.values)
특성 스케일링
- 데이터에 적용할 가장 중요한 변환 중 하나가 특성 스케일링입니다. 입력 숫자 특성들의 스케일이 많이 다르면 잘 동작하지 않습니다.
- 즉, 전체 방 개수의 범위는 6에서 39,320인 반면에 중간 소득의 범위는 0에서 15까지인 경우가 예시로 들 수 있겠습니다.
- 스케일링을 하는 방법은 min-max 스케일링(정규화)이 가장 간단합니다, sklearn에서는 MinMaxScaler 변환기를 제공한다.
-> 0~1 범위에 들도록 값을 이동하고 스케일을 조정하면 된다, 데이터에서 최솟값을 뺀 후 최대값과 최솟값의 차이를 나누면 이렇게. 할 수 있다. - 하지만 표준화는 다릅니다. 먼저 평균을 뺀 후 표준편차로 나눠 결과 분포의 분산이 1이 되도록 합니다.
-> sklearn에서 StandardScaler 변환기 제공
변환 파이프라인
앞에 있었던 내용들을 순서대로 실행해야합니다.
- sklearn에는 연속된 변환을 순서대로 처리할 수 있도록 도와주는 Pipeline 클래스가 있습니다.
- Pipline 클래스를 이용하면 여러 작업을 Pipline 으로 설정하여 마지막에 fit_transform 메서드로 차례로 작업을 진행합니다.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# StandardScaler: 분산 1을 갖도록 변환하는 표준화 스케일링 함수
# 이 객체는 여러 단계의 데이터 전처리를 연속적으로 적용할 수 있도록 도와주며 이름과 해당 단계를 지정한다.
num_pipeline = Pipeline([
# 빈 값을 대체할 값을 중간값으로 설정한다.
('imputer', SimpleImputer(strategy="median")), #imputer.fit(데이터값)해야함
# 새로운 특성을 추가하는 작업을 수행 하지만 여기서는 추가안하는듯, 이 작업을 attribs_adder라는 이름으로 지정
('attribs_adder', CombinedAttributesAdder()),
# 데이터의 표준화를 수행하는 작업을 수행한다. std_scaler라는 이름으로 작업 이름 지정하고 StandardScaler 객체를 사용
('std_scaler', StandardScaler()),
])
# 파이프라인을 훈련 데이터셋인 housing_num(범주형특성을 제외한 계층적샘플링을 통해 선별한 값)에 적용
# 즉 위에서 3가지 작업을 연속으로 지정할 전처리를 housing_num을 대상으로 하여
# 작업이 끝난 값을 housing_num_tr에 넣는다.
# fit_transform: 데이터를 학습하고 주어진 데이터를 변환하는 것이다.
housing_num_tr = num_pipeline.fit_transform(housing_num)# num_pipeline를 활용한다.
# 1.비어있는 값을 중간값으로 설정한다.
# 2.새로운 특성을 추가한다. (rooms_per_household, population_per_household)
# 3.표준화 알고리즘으로 데이터를 스케일링한다.
housing_num_tr
이제 full_pipeline을 만듭니다. 위에서 만들어준 Pipline과 OneHotEncoding을 동시에 작업할 수 있도록 sklearn에서 제공하는 ColumnTransformer가 추가되었습니다.
- ColumnTransformer를 사용하여 fit_transform 를 해줌으로 파이프라인을 훈련시킴과 동시에 housing 데이터를 변환할 수 있다.
from sklearn.compose import ColumnTransformer
#scikit-learn 라이브러리에서 ColumnTransformer 클래스를 가져온다
#ColumnTransformer는 데이터프레임의 열에 대한 다양한 전처리 단계를 쉽게 적용할 수 있도록 도와주는 도구다
#list는 데이터프레임 또는 배열의 모든 열을 리스트 형태로 변환한다.
#ocean_procimity 값이 빠진 수치형 특성의 열 이름을 저장
num_attribs = list(housing_num)
#범주형 특성인 ocean_proximity 열에 대해 OneHotEncoder를 사용하여 원핫 인코딩 수행
cat_attribs = ["ocean_proximity"]
#특성의 열에 따라 맞는 처리를 위해(즉, 숫자 변환, 텍스트/범주 변환)
#ColumnTransformer 클래스 활용
full_pipeline = ColumnTransformer([
# 위에서 만든 num_pipline을 사용하여 num_attribs에 포함된 숫자형 특성들을 전처리한다.
("num", num_pipeline, num_attribs),
# OneHotEncoder를 사용하여 ocean_proximity 열을 원-핫인코딩한다.
("cat", OneHotEncoder(), cat_attribs),
])
#원본 데이터프레임을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터를 Housing_prepared에 넣는다.
housing_prepared = full_pipeline.fit_transform(housing)
모델 훈련
위에 과정을 통해 따라오면 이제 모델을 사용하여 데이터 훈련시킬 수 있습니다.
1. 먼저 선형 회귀 모델 알고리즘인 LinearRegression()를 사용하여 전처리가 끝난 데이터와 정답을 가지고 모델을 생성 및 학습시킵니다
from sklearn.linear_model import LinearRegression
#선형 회귀 모델을 생성한다.
lin_reg = LinearRegression()
#housing_prepared: 원본 데이터프레임을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터를 Housing_prepared에 넣는다.
#housing_labels: 계층적샘플링을 통해서 얻은 실제집값
#선형 회귀 알고리즘으로 학습시킨다.
# fit은 훈련 -> 모델 파라미터를 찾아낸다.
# housing_prepared: 전처리가 끝난 데이터, housing_labels: 레이블(정답,실제 집값)데이터
lin_reg.fit(housing_prepared, housing_labels)
#값을 예측하는 모델을 만든 것이다.
2. 선형 회귀 알고리즘으로 훈련된 모델을 사용해 값을 예측해봅니다
- 원본 데이터 프레임에서 5개의 값만 뽑아서 값을 예측하는 것입니다.
# let's try the full preprocessing pipeline on a few training instances
# 전체 데이터셋에서 5개 인스턴스를 가지고 학습한 모델에 적용하여 결과값 예측
#some_data: 원본 데이터프레임에서 처음 5개의 데이터 행을 선택하여 저장한다.
some_data = housing.iloc[:5]
#some_labels: 학습 데이터에 대한 실제 타겟값을 나타내는 housing_labels에서 처음 5개의 레이블을 선택하여 저장
#some_labels는 모델이 예측한 결과와 비교하기 위한 실제값이다.
#계층적샘플링을한 것
some_labels = housing_labels.iloc[:5]
#전처리 파이프라인을 사용하여 some_data에 대한 전처리를 수행하고 전처리된 데이터를 저장한다.
some_data_prepared = full_pipeline.transform(some_data)
#선형 회귀 알고리즘을 사용하여 fit(훈련)된 lin_reg 모델을 사용하여 predict(예측)을 수행
#lin_reg 모델을 사용하여 some_data_prepared에 대한 예측을 수행하고 예측값을 출력한다.
print("Predictions:", lin_reg.predict(some_data_prepared))#실제 집값으로 전처리 파이프라인을 사용해 전처리한 데이터를 가지고 선형회귀 모델로 예측한 값과
#아래에 비교하기 위한 실제 집값을 의미한다.
print("Labels:", list(some_labels))
지금까지 한 작업들을 간략하게 정리하면
-> 중위소득이 집값을 예측하는데 매우 중요하다고 해서 중위소득(정답 레이블)을 제외한 특징들을 가공(전처리)한다
-> 가공된 특징 데이터들을 가지고 머신러닝 알고리즘 모델을 만들어 모델을 학습시킨다.
-> 중위소득을 기반으로 집값을 예측하는 모델을 만들었으면 그 모델에 값을 넣어서 테스트셋 값을 예측해보라고 시킨다.
-> 중위소득을 기반으로 집값을 예측하도록 훈련된 모델이 테스트셋 값으로 예측한 집값을 출력한다.
하지만 첫 번째 문장을 보면 중위 소득이 집값을 예측하는데 매우 중요하다고 해서 중위 소득을 기반으로 데이터를 가공해서 모델을 훈련시켰지만 만약에 중위 소득이 아니라 다른 특성이 더 집값하고 긴밀한 관계가 있다고 하면 문제가 발생합니다.
- 그래서 피어슨의 r 을 사용해서 상관관계를 파악하는 것입니다.
- 만약 새로운 특성을 만들었는데 해당 특성이 중위 소득보다 더 상관관계가 깊다면? 그 특성을 기반으로 다시 데이터를 가공하고 모델을 훈련시킨 후 훈련된 모델로 값을 예측하면 됩니다.
모델의 측정값 RMSE로 평가
모델을 훈련하고 훈련된 모델로 집값을 예측해봤으면 이제 그 값이 얼마나 정확한지, 오류가 어느정도 있는지를 확인해야힙니다.
- 그러기 위해서는 평균 오차 제곱근을 구해서 평균적인 오차 범위를 구할 수 있습니다.
- full_pipeline 을 통해서 가공이 끝난 원본 데이터(housing_prepared)로 값을 예측해서 housing_predictions 에 값을 넣습니다.
- 계층적샘플링으로 나눈 집값(즉 정답 레이블)과 housing_predictions(예측한 값)을 가지고 평균 오차 제곱을 구합니다.
- 평균 오차 제곱을 구한 값에 제곱근(sqrt)를 씌워서 RMSE 로 변환합니다 -> RMSE 의 값은 68633.40810776998 이 나옵니다.
RMSE: 회귀(regression) 문제에서 사용하는 전형적인 성능 지표
from sklearn.metrics import mean_squared_error
#mean_squared_error로 평균 오차 제곱을 구하고
#sqrt를 하여 평균 오차 제곱 근을 구해 평균적인 오차 범위를 알 수 있다.
#housing_prepared는 원본 데이터프레임(housing)을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터
#lin_reg 선형회귀 모델을 사용하여 학습 데이터에 대한 예측을 수행하고, 이 예측값을
#housing_predictions에 저장한다. 즉, 모델이 학습 데이터에 대한 주택 가격 예측을 수행한 결과
#array([[-0.94135046, 1.34743822, 0.02756357, ..., 0. ,0. , 0. ] 이런 값들을 가지고 계산해준다.
housing_predictions = lin_reg.predict(housing_prepared)
#housing_labels: 계층적샘플링으로 나눈 집값
#housing_predictions: 원본 데이터를 선형회귀 모델로 값을 구한 집값
#함수를 사용하여 예측값과 실제값 사이의 평균 제곱 오차를 계산한다.
#lin_mse는 예측 오차의 제곱을 모든 데이터 포인트에 대해 평균한 값
lin_mse = mean_squared_error(housing_labels, housing_predictions) # 둘이 순서 바꿔도 똑같다
#계산된 mse값을 제곱근을 씌워서 RMSE로 변환
lin_rmse = np.sqrt(lin_mse)
#실제 중간 주택 가격과 약 $68633 오차가 있다는 것을 의미한다. 줄일수록 좋은것
lin_rmse #
위에서는 오차범위가 68633이나 되며 이를 해결하기 위해서는 더욱 강력한 모델을 사용하는 방법이 있습니다.
아래는 결정 트리 회귀 모델을 사용한 것이고 훈련 방법은 선형 회귀하고 똑같습니다.
- 값이 매번 랜덤하지 않도록 seed값을 42로 설정합니다.
- full_pipeline 을 거쳐서 가공(전처리)된 housing_prepared 데이터로 계층적샘플링으로 구한 housing_labels(실제 집값)을 맞추도록 학습시킵니다.
from sklearn.tree import DecisionTreeRegressor
#선형회귀모델은 약해서 언더피팅 모델이다.
#그러기 위해서 더 강력한 모델인 결정 트리 회귀 모델을 사용하는 것이다.
tree_reg = DecisionTreeRegressor(random_state=42)
# housing_prepared: 전처리가된 원본 데이터
# 계층적 샘플링으로 나눈 집값 (답안지라고 부르심)
tree_reg.fit(housing_prepared, housing_labels)
# 값을 예측하기 위한 모델 만들기, 모델.fit(x(i)값, y(i)값)
위에서 훈련된 데이터로 값을 예측한 값으로 평균 오차 제곱근을 구하면 값이 0이라는 값이 나오는데 이는 의심해봐야하는 상황입니다.
#housing_prepared: 전처리된 원본 데이터
housing_predictions = tree_reg.predict(housing_prepared)
# h(x) = housing_labels, y=housing_predictions
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
교차검증
교차 검증을 통해서 학습 모델을 평가할 수 있습니다.
교차 검증이란?
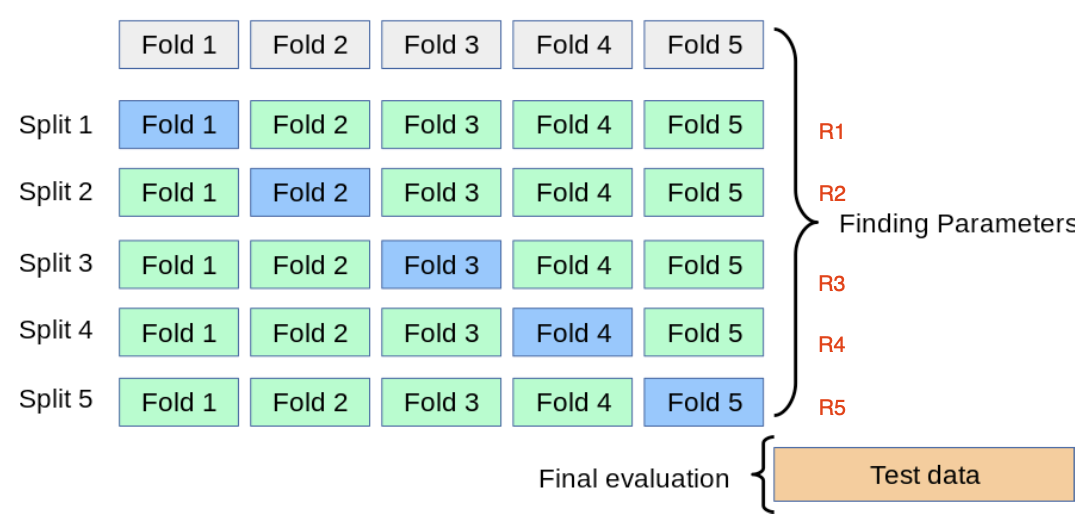
- 훈련셋을 k-폴드로 나눕니다
- k-1 폴드를 이용해서 ML 모델을 훈련하고 나머지 폴드를 이용해 모델 성능을 검증합니다
- 위 과정을 k번 반복하여 최적의 파라미터 (모델, 하이퍼파라미터)를 찾아 모델 확정합니다
- sklearn에서 k-폴드 교차 검증 CV 함수인 cross_val_score 를 제공하고 있습니다.
모델마다 다른 결과
추가로 아래를 확인했을 때와 같이 모델도 종류마다 성능이 다릅니다.
#lin_reg: 선형회귀 모델을 사용해서 얻은 결과값
#housing_prepared는 전처리된 주택 데이터의 특성들, 교차 검증에 사용할 데이터셋
#housing_labels는 계층적샘플링을 통해서 얻은 집값들로 답안지
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)

아래는 결정회귀 회귀 모델을 사용한 코드입니다.
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
tree_reg = make_pipeline(preprocessing, DecisionTreeRegressor(random_state=42))
tree_reg.fit(housing, housing_labels)
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
#tree_rmse_scores = np.sqrt(-scores): 교차 검증에서 계산된 음수 MSE를 다시 양수로 변환하고 루트를 씌워 제곱근 RMSE값을 계산한다.
tree_rmse_scores = np.sqrt(-scores)
앞에 선형회귀 모델을 사용했을떄 RSME가 $2,731 이였지만, 교차 검증을 통해서 확인해본 결과 평균오차가 $71,407, 표준편차가 $2,439라는 것을 확인할 수 있습니다.
#교차검증을 통해서 얻은 결과값
def display_scores(scores):
print("Scores:", scores) # 점수
print("Mean:", scores.mean()) # 평균
print("Standard deviation:", scores.std()) # 표준편차
display_scores(tree_rmse_scores)
'AI > Machine Learning' 카테고리의 다른 글
| 사이킷런 scikit-learn 이란? (0) | 2024.07.09 |
|---|---|
| 여러 개의 레이블을 갖는 하나의 데이터 분류하기 - 다중 레이블 분류 (2) | 2024.07.08 |
| 머신러닝 분류 (숫자 예측) (0) | 2024.07.07 |
| 머신러닝 모델 튜닝하기 (0) | 2024.06.28 |
| 머신러닝 시작하기 (0) | 2024.06.26 |

실제 데이터로 작업하기
머신러닝을 배울 때는 인공적으로 만들어진 데이터셋이 아닌 실제 데이터로 실험해보는 것이 가장 좋습니다.
현재 여러 분야에 걸쳐 공개된 데이터셋이 아주 많이 존재합니다. 다음은 데이터를 구하기 좋은 곳입니다.
- 유명한 공개 데이터 저장소
- UC 얼바인 머신러닝 저장소 (http://archive.ics.uci.edu/ml)
- 캐글 데이터셋 (http://www.kaggle.com/datasets)
- 아마존 AWS 데이터셋(https://registry.opendata.aws) - 메타 포털(공개 데이터 저장소가 나열되어 있습니다)
- 데이터 포털 (http://dataportals.org)
- 오픈 데이터 모니터 (http://opendatamonitor.eu)
- 퀸들 (http://quandl.com) - 인기 있는 공개 데이터 저장소가 나열되어 있는 다른 페이지
- 위키백과 머신러닝 데이터셋 목록 (https://goo.gl/SJHN2K)
- Quora.com (https://homl.info/10)
- 데이터셋 서브레딧 (http://www.reddit.com/r/datasets)
캘리포니아 주택 가격 예측 프로젝트
이번 포스팅에서는 캘리포니아 주택 가격 데이터셋을 사용할 것입니다. (데이터셋 다운받기)

캘리포니아 주택 집값을 예측할 수 있는 프로젝트를 진행한다고 가정을 해봅니다.
부동산 회사에 고용된 데이터 과학자로서 할 일은?
- 캘리포니아 인구조사 데이터를 사용하여 캘리포니아 주택 가격 모델 생성을 합니다
- 생성한 모델한테 새로운 측정 데이터를 주었을 때, 해당 구역의 중간 주택 가격을 예측할 수 있게 만들어야 합니다
- 데이터셋에 대한 분석이 필요합니다.
- 캘리포니아의 블록그룹마다 인구, 중간 소득, 중간 주택 가격, 위도, 경도 등 여러 특성들이 존재하고 있습니다.
블록그룹이란 미국 인구조사국에서 샘플 데이터를 발표하는데 사용하는 최소한의 지리적 단위(하나의 블록은 보통 600~3000명 포함)
- 무엇보다 프로젝트를 진행하기 전에 주택 모델 생성의 최종 목적이 무엇인가를 파악하는 것이 매우 중요합니다.
✓ 알고리즘 선택, 모델 평가를 위한 성능 지표 선택, 모델 조정 (tweaking)을 위한 시간 투자 등 결정 요소
문제 정의
- 작업 목적에 맞게 ML 시스템을 설계해야 합니다 -> 집값을 예측하기 위해서는 어떤 학습을 통해 모델을 만들어야 할까?
Q: 지도, 비지도, 준지도, 강화 학습?
✓ A: 레이블 된 훈련 샘플 (각 구역 별 중간 주택 가격이 제시됩니다) -> 지도 학습
Q: 분류 작업, 회귀 작업?, 지도 학습에서 어떤 알고리즘을 사용해야 할까?
✓ A: 주어진 구역의 중간 주택 가격을 예측 -> 회귀 작업
Q: 배치 학습, 온라인 학습?
✓ A: 빠르게 변하는 데이터에 적응 하지 않음 -> 배치 학습 (오프라인 학습)
성능 측정 지표 선택
- 모델 학습을 위한 성능 측정 지표 선택
✓ (학습하는 동안) 모델의 예측 결과에 얼마만큼의 오차가 있는가?
✓ 예로서, 모델이 예측한 주택 값과 레이블로 주어진 실제 값 사이에 오차가 커질 수록 예측에 얼마나 오류가 있는지 확인가능 - RMSE (root mean square error, 평균 제곱근 오차)
✓ 회귀 (regression) 문제에서 사용하는 전형적인 성능 지표입니다
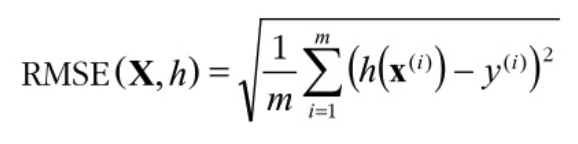
RMSE (Root Mean Square Error) 란
Error(에러) 값에 (Square)제곱을 한 후 Mean(평균) 값을 구한 다음 Root(제곱근)을 씌우는 것입니다.
RMSE는 평균 제곱근 오차라고 불리며 실제 값과 예측 값의 오차를 나타내는 정도입니다. 즉 예측에 오류가 얼마나 많이 있는지를 가늠하게 해줍니다. 물론 값이 작으면 작을수록 좋습니다.
RMSE에서 수식을 분석해보겠습니다.

- m: 인스턴스의 수 (행), ex. 인스턴스1: (경도, 위도, 거주자수, 중간 소득, •••)
- x(i): i 번째 인스턴스의 전체 특성값 벡터
- y(i): i 번째 인스턴스의 기계가 예측한 전체 특성값 벡터
- X: RMSE(X,h)에서 X는 데이터셋의 모든 인스턴스 특성값들을 포함하는 행렬(레이블 제외)
- h: 가설, 즉 기계가 백터 값으로 예측값을 출력할 수 있도록 만드는 예측 함수
- 만약 h(x(1)) = (-118.29, 33.91, 1,416, 38,372 •••) 이면 h(예측 함수)로 값을 계산(예측)을 합니다 (158,400)
- 마지막으로 수식의 1부터 m까지의 값을 모두 (h(x(i) - y(i))^2의 구해 평균을 구하면 평균 제곱근 오차 값을 구할 수 있게 됩니다.
데이터 준비하기
데이터를 학습하고 예측하기 위해서는 아나콘다 쥬피터 노트북 또는 VScode처럼 작업할 수 있는 환경이 필요로 합니다.
데이터 가져오기
1. 기본 설정 후 학습할 데이터와 학습한 데이터를 기반으로 테스트할 데이터를 가져옵니다.
import os #Python의 내장 모듈 중 하나로, 파일 및 디렉터리 관리를 위한 함수와 클래스를 제공합니다.
import tarfile #Python의 내장 모듈 중 하나로, tar 파일을 조작하기 위한 함수와 클래스를 제공합니다.
import urllib.request #URL을 통해 데이터를 다운로드하기 위한 모듈입니다.
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/" #데이터를 다운로드할 기본 URL을 지정합니다
HOUSING_PATH = os.path.join("datasets", "housing") #데이터를 저장할 로컬 디렉터리 경로를 설정합니다
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz" #다운로드할 데이터 파일의 URL을 설정합니다
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH): #데이터를 다운로드하고 압축을 해제하는 함수
if not os.path.isdir(housing_path): #가능하지 않은 디렉터리위치라면
os.makedirs(housing_path) #디렉터리를 만든다.
tgz_path = os.path.join(housing_path, "housing.tgz") #다운로드한 파일을 저장할 경로와 저장할 파일이름 지정
urllib.request.urlretrieve(housing_url, tgz_path) #지정된 URL에서 데이터 파일을 다운로드 후 tgz_path 경로에 저장
housing_tgz = tarfile.open(tgz_path) #다운로드한 tar 파일 열기
housing_tgz.extractall(path=housing_path) #tar 파일을 압축 해제 후 압축 해제된 파일들을 housing_path 디렉터리에 저장
housing_tgz.close() #tar 파일 닫기fetch_housing_data()
가져온 데이터 저장하고 읽어오기
fetch_housing_data 메서드를 사용하여 가져온 csv 파일을 가져오는 메서드를 만듭니다.
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv") #housing_path 경로에 housing.csv를 추가
return pd.read_csv(csv_path) #지정한 디렉터리 위치에 있는 housing.csv 파일읽기
데이터가 어떻게 되어 있는지 확인하기
데이터를 housing 변수로 담아낸 후 head 메서드를 사용하여 최초 5개의 행을 출력합니다.
housing = load_housing_data() #함수를 호출하여 데이터셋을 로드하고, 그 결과를 housing 변수에 저장합니다. 이렇게 하면 데이터셋이 메모리에 로드되고 데이터프레임 형태로 저장됩니다.
housing.head() #데이터프레임의 처음 다섯 개의 행을 출력
#head() 메서드는 데이터프레임의 상위 몇 개의 행을 반환하고,기본적으로 처음 다섯 개의 행을 반환
housing.info() #데이터프레임인 housing의 정보를 요약하여 보여주는 메서드
info를 통해 확인해보면 다음과 같이 데이터를 분석할 수 있습니다.
- 데이터셋에 20,640 인스턴스가 있음을 확인할 수 있습니다
- 207개 인스턴스는 total_bedrooms 특성이 없습니다
- ocean_proximity 특성을 제외한 나머지는 모두 숫자형입니다 (float64)
- ocean_proximity 특성은 값이 반복되므로 범주형 특성입니다 (텍스트)

데이터 시각화
데이터를 시각화하여 확인하면 좀 더 직관적으로 분석할 수 있게 됩니다.
시각화를 위해서는 여러 라이브러리가 있으며 다음은 matplotlib를 사용하여 시각화를 한 결과입니다.
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(12, 8))
plt.show()
데이터를 확인했을 때 데이터에 상한 (upper limit)이 있음을 확인할 수 있습니다.
추가로 중간 소득 특성 ($)이 스케일링 되었음을 확인할 수 있습니다. -> 0~50$면..

가져온 데이터 무작위 셔플링
가져온 데이터를 그냥 사용하기보다 무작위로 섞는 과정을 진행합니다. 무작위로 섞어서 훈련셋과 테스트셋을 나눕니다.
np.random.seed(42) #42를 시드로 설정한다, 발생되는 랜덤 값을 예측할 수 있다.
np.random.rand(5) #시드값은 보통 시간 등을 사용해 설정하지만 사람이 수동으로 설정할 수도 있다.import numpy as np
# For illustration only. Sklearn has train_test_split()
def split_train_test(data, test_ratio): #데이터와 테스트셋의 비율을 인자로 받는다.
shuffled_indices = np.random.permutation(len(data)) #데이터 인덱스를 무작위로 섞은 배열을 생성, permutation: 순열, 몇 개를 골라 순서를 고려해 나열한 경우의 수
test_set_size = int(len(data) * test_ratio) #테스트 세트의 크기를 결정
test_indices = shuffled_indices[:test_set_size] #섞인 인덱스 배열에서 처음부터 test_set_size까지의 인덱스를 추출하여 테스트 세트의 인덱스로 설정
train_indices = shuffled_indices[test_set_size:] #테스트 세트로 선택되지 않은 나머지 데이터를 섞어 훈련 세트로 사용하는 것을 의미
return data.iloc[train_indices], data.iloc[test_indices] #함수는 훈련 세트와 테스트 세트를 데이터프레임 형태로 반환
# 무작위로 뽑은 훈련셋,테스트셋
train_set, test_set = split_train_test(housing, 0.2) #테스트셋 비율을 0.2로 설정
len(train_set) #훈련셋의 크기를 확인한다. # 16512
len(test_set) #데이터셋의 크기를 확인한다. # 4128
위에는 무작위로 테스트셋과 훈련셋 나누는 작업을 직접 구현하였지만 sklearn에서는 train_test_split 클래스를 제공합니다.
sklearn 에서 제공하는 train_test_split 을 사용하면 별 다른 구현 없이 데이터를 테스트셋과 훈련셋으로 나눌 수 있습니다.
from sklearn.model_selection import train_test_split
# 난수를 이용하여 랜덤하지 않게 훈련셋과 테스트셋으로 나눈다.
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
무작위로 샘플링했을 때 발생하는 문제점
위에서 train_test_split 메서드로 무작위로 테스트셋과 훈련셋을 나눴지만 무작위로 나누면 편향될 수 있습니다.
- 만약에 전문가가 중간 소득이 중간 주택 가격을 예측하는데 매우 중요하다고 얘기했다는 가정을 해본다면 이 경우 테스트 셋이 전체 데이터셋에 있는 여러 소득 카테고리를 잘 대표해야 합니다.
- 중간 소득은 수치형 특성이므로 소득에 대한 카테고리 특성을 만들어야 합니다.
- 중간 소득 대부분은 $15,000~$60,000 사이에 모여 있지만 일부는 $60,000를 넘기기도 합니다.
- 계층별로 데이터셋에 충분한 샘플 수가 있어야지 아니면 계층의 중요도를 추정하는데 편향이 발생한다는 것 즉 -> 계층을 너무 많이 나누면 안되고 각 계층이 충분히 커야 합니다(양).
해결 방법 (계층적 샘플링)
위처럼 무작위 샘플링을 통해 편향적인 데이터셋을 만들어내는 것에 해결할 수 있는 방법은 전체 데이터셋에서 무작위로 데이터를 뽑는 것이 아닌 비율에 따라서 뽑는 방법을 사용할 수 있겠습니다. -> 계층적 샘플링이라고 불립니다.
물론 sklearn에서는 이런 작업을 대신 해주는 메서드를 만들었으며 그것이 바로 StratifiedShuffleSplit() 메서드입니다.
# median_income 특성을 이용해서 소득을 나눌 구간(bins)를 설정하고 각 구간에 대응하는 카테고리 레이블을 정의한다.
housing["income_cat"] = pd.cut(housing["median_income"], #median_income 열을 기반으로 income_cat 열을 생성한다.
bins=[0., 1.5, 3.0, 4.5, 6., np.inf], #소득을 나눌 구간(카테고리)을 정의, 0에서 1.5, 1.5에서 3.0, 3.0에서 4.5, 4.5에서 6.0 그리고 6.0 이상의 다섯 개의 구간을 설정한다.
labels=[1, 2, 3, 4, 5]) #각 구간에 대응하는 카테고리 레이블을 정의한다. 구간에 따라 소득 카테고리가 1부터 5까지 할당된다.- 먼저 income_cat 이름의 적당한 계층 개수로 특성을 만들었습니다.
- 카테고리를 1, 2, 3, 4, 5로 나누고, 카테고리 1은 0에서 1.5까지 범위(즉$15,000 이하)이고 카테로기 2는 1.5에서 3까지 범위가 되는 식입니다
- 무작위로 막 뽑기에는 2~6 구간이 너무 많아서 그쪽 소득으로 편향될 가능성이 있기 때문에 계층으로 나눠 각 계층에서 일정 몇%씩 뽑는 그런 메커니즘으로 진행하면 공정해집니다.
-> 즉 방금 한 구간나누기는 계층적 샘플링을 하기 위해서 각 값이 본인의 카테고리를 잘 대표할 수 있도록 구간을 나눈 것


이제 위에서 만든 소득 카테고리를 기반으로 계층적샘플링을 할 준비가 끝났습니다.
- 계층적샘플링이란? -> 자신이 속한 구간을 잘 대표하는 데이터들을 편향하지 않게 잘 뽑는 것입니다.
중간소득을 기반으로 만든 카테고리 특성을 sklearn의 StratifiedShuffleSplit을 사용하여 계층 샘플링을 할 차례입니다.
from sklearn.model_selection import StratifiedShuffleSplit #계층적 셈플링
# 데이터를 분할하는 횟수=1, 테스트셋 비율=0.2, 난수 초기값을 설정
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
#위에서 설정한 계층적 샘플링 객체인 split에 split메서드를 사용하여 housing 데이터에서 새로만든 소득 카테고리를 가지고 계층적 샘플링을 한다
for train_index, test_index in split.split(housing, housing["income_cat"]): # housing데이터프레임에서 imcome_cat을 사용하여 분할, split메서드를 호출하여 데이터를 분할한다.
strat_train_set = housing.loc[train_index] #계층적셈플링 훈련셋 ,loc: pandas 라이브러리에서 데이터프레임에서 특정 행을 선택하거나 조건에 맞는 데이터를 인덱싱하는 기술
strat_test_set = housing.loc[test_index] #계층적셈플링 테스트셋
# loc:열만 가져오기, df.loc[칼럼슬라이싱]#이를 통해 전체 데이터셋에서 각 소득 카테고리가 차지하는 비율을 확인할 수 있다.
housing["income_cat"].value_counts() / len(housing) #income_cat열의 각 소득 카테고리별 데이터 포인트 비율을 계산하는 코드다.

계층적샘플링을 했을때와 무작위로 뽑았을때 나타나는 오류 오차범위를 확인할 수 있습니다.
-> 확인결과 랜덤으로 뽑을때 비율이 방금 계층 샘플링으로 만든 housing["income_cat"]보다 부정확하다는 것을 확인 할 수 있습니다
def income_cat_proportions(data): #소득 카테고리별 데이터 포인트 비율을 계산하는 함수
return data["income_cat"].value_counts() / len(data)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({
"Overall": income_cat_proportions(housing),#각 소득 카테고리별 데이터 포인트 비율얻기
"Stratified": income_cat_proportions(strat_test_set),#각 소득 카테고리별 데이터 포인트 비율얻기
"Random": income_cat_proportions(test_set),#무작위 샘플링으로 생성된 소득 카테고리별 데이터 포인트 비율얻기
}).sort_index() #Overall:전체 데이터셋, Stratified: 테스트셋, Random: 랜덤 테스트셋
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100compare_props


- 계층 샘플링(구간을 나눠)을 사용해 만든 테스트셋의 소득 카테고리 비율이 전체 데이터셋 비율과 가까운 것을 확인할 수 있다.(공평)
계층적 샘플링을 통해서 데이터도 잘 뽑았겠다 이제 사용한 (방금 만들었던) income_cat 열을 지워줍니다.
for set_ in (strat_train_set, strat_test_set):
#axis=0: 행삭제, axis=1: 열삭제
set_.drop("income_cat", axis=1, inplace=True)
계층적 샘플링 후 시각화
계층적샘플링을 통해서 분리한 훈련셋을 이용해 시각화를 합니다.
#복사를 해서 사용하는 이유는 기존 훈련셋을 손상시키지 않기 위해 복사본을 만드는 것이다.
housing = strat_train_set.copy() #계층 샘플링을 사용해 만든 테스트셋, copy()는 값만 복사하는 것, 참조 Xhousing.plot(kind="scatter", x="longitude", y="latitude")
save_fig("bad_visualization_plot") #생성된 시각화를 파일로 저장하기
하지만 위는 안좋은 시각화 파일입니다. 좋은 시각화 파일을 만들려면 투명도를 설정해야합니다.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
save_fig("better_visualization_plot")
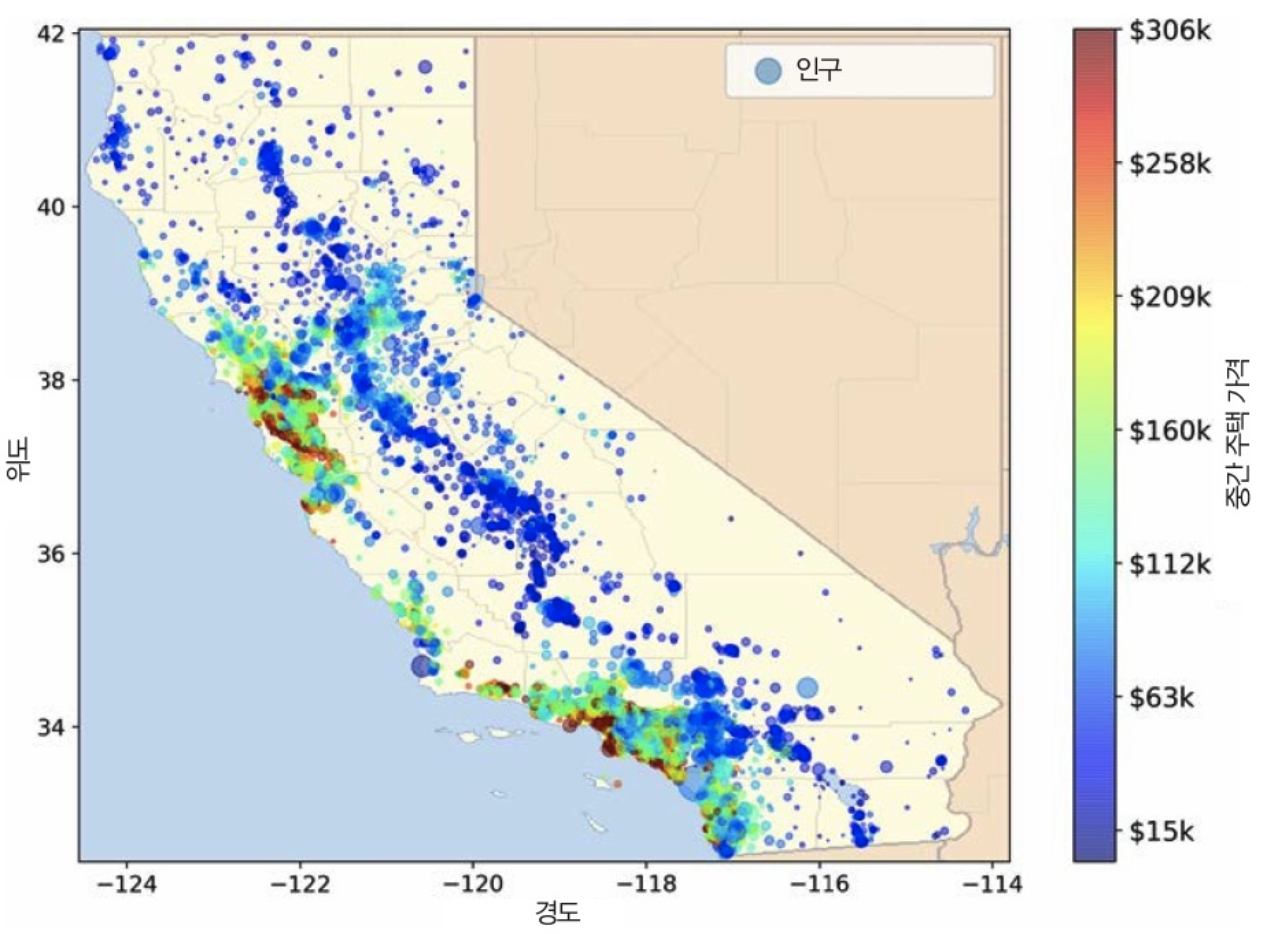
다음처럼 설정하면 그래프 유형, 축 이름, 컬러맵, 투명도 등을 설정하여 데이터 시각화 할 수 있습니다
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()
save_fig("housing_prices_scatterplot")
상관관계
다음으로 상관관계 corr()를 조사해야합니다. 피어슨의 r 이라고 불리는 표준 상관 계수는 -1 < r < 1 의 범위를 갖습니다.
- 1에 가까우면 강한 양의 상관관계 (예: 중간 주택 가격이 상승하면 중간 소득도 증가하는 경향)
- -1에 가까우면 강한 음의 상관관계 (예: 위도가 올라갈 수록 중간 주택 가격은 조금씩 내려가는 경향)
- 특징으로는 상관계수는 선형적인 상관관계만 측정할 수 있으며 비선형적인 상관관계는 측정할 수 없습니다
corr_matrix = housing.corr(numeric_only=True) #각 열(특성) 간의 상관 관계를 계산한다.
corr_matrix
상관관계의 값에 따라 데이터는 여러 형태로 존재할 수 있습니다.

corr_matrix["median_house_value"].sort_values(ascending=False)
#"median_house_value" 열과 다른 모든 열 간의 상관 관계를 가져와 내림차순으로 정렬
다음은 상관계수를 시각화한 결과입니다.
# from pandas.tools.plotting import scatter_matrix # For older versions of Pandas
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"] # 4x4
scatter_matrix(housing[attributes], figsize=(12, 8))# 선택한 특성 간의 모든 산점도를 생성한다. 그림 크기 설정
save_fig("scatter_matrix_plot")
- 중간 주택 가격(median_house_value)을 예측하는데 가장 유용할 것 같은 특성을 중간 소득(median_income)이므로 상관관계 산점도를 확대대하여 분석해봅니다.
✓ 위에서 상관관계는 선형적인 상관관계만 측정할 수 있다고 하였는데 아래에서
housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
plt.axis([0, 16, 0, 550000]) # 가격 제한 50000이나 이상한 데이터를 학습하지 않게 제거작업이 필요할 수 있다.
save_fig("income_vs_house_value_scatterplot")
- 상관관계가 매우 강하다는 것을 알 수 있으며
- 1. 위쪽으로 향하는 경향을 볼 수 있고, 포인트들이 너무 널리 퍼져 있지 않음 -> 수직일수록 좋고 주변에 지져분한게 없어야 좋음.
- 2. 앞서 본 가격 제한값이 $500,000에서 수평선을 잘 보임.
이렇게하여 median_income 과 median_house_value 가 집값을 예측하는데 관계가 높음을 알 수 있습니다.
특성 조합하기 (특성공학)
특성을 조합해서 집값을 예측할 수 있는 유의미한 새로운 특성을 만들 수 있습니다.
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]
새로 만든 특성들과 median_house_value (중간 주택 가격)과의 상관관계(피어슨의 r)을 확인해보고 유의미성을 확인합니다.
corr_matrix = housing.corr() # 새로운 조합으로 만들어진 특성간의 상관관계 파악
corr_matrix["median_house_value"].sort_values(ascending=False)
새로 만든 특성들이 추가된 상태에서 새로 상관관계를 출력합니다.
- 새로운 rooms_per_household는 양의 상관관계를 보이고
- 새로운 bedrooms_per_room은 음의 상관관계를 보이고
- 새로운 population_per_household도 음의 상관계수를 보입니다.
이후 새로운 rooms_per_household 특성과 중간 주택 가격의 산점도(시각화)로 상관관계도 파악해볼 수 있습니다.
# 특성을 조합해서 새로운 특성을 가지고 그림그리기
housing.plot(kind="scatter", x="rooms_per_household", y="median_house_value",
alpha=0.2) # x축의 데이터 값을 rooms_per_household, y축의 데이터 값을 median_house_value 값으로 설정
plt.axis([0, 5, 0, 520000])
#x축은 0에서 5까지, y축은 0에서 520,000까지의 범위로 지정합니다. 이렇게 범위를 설정함으로써 산점도의 축의 스케일을 조절할 수 있습니다
plt.show()
데이터 정제
머신러닝 알고리즘을 위한 데이터를 준비해야하는데 이 작업은 수동으로 하는 대신 함수를 만들어서 자동화를 해야합니다. 이유는
* 어떤 데이터셋에 대해서도 데이터 변화을 손쉽게 반복할 수 있습니다. (다음에 새로운 데이터셋을 사용할 때)
* 향후 프로젝트에 사용할 수 있는 변환 라이브러리를 점진적으로 구축할 수 있습니다.
* 실제 시스템에서 알고리즘에 새 데이터를 주입하기 전에 변환시키는 데 이 함수를 사용할 수 있습니다.
* 여러 가지 데이터 변환을 쉽게 시도해볼 수 있고 어떤 조합이 가장 좋은지 확인하는 데 편리합니다.
다음은 레이블 데이터에 같은 변형을 적용하지 않기 위해 훈련 데이터셋에서 레이블(정답)을 분리해서 따로 저장하는 것입니다
# drop은 지우는 것이 아니라 해당 값만 임시로 뺀다는 것이다, axis=1은 열을 기준으로 삭제하라는 의미
housing = strat_train_set.drop("median_house_value", axis=1)
#데이터프레임에서 median_house_value 열만 선택하여 housing_labels 시리즈에 저장
housing_labels = strat_train_set["median_house_value"].copy()
NULL 값 대응하기
다음으로 housing에서 null 값이 들어있는 행을 나타냅니다.
sample_incomplete_rows = housing[housing.isnull().any(axis=1)].head()
sample_incomplete_rows
비어있는 null값이 들어있는 데이터를 가지고 모델을 훈련하게 될 경우 오류가 날 수 있습니다.
해결할 수 있는 방안에는 다음 3가지가 있습니다.
1. 비어있는 해당 인스턴스를 제거한다.
sample_incomplete_rows.dropna(subset=["total_bedrooms"]) # option 1: 해당 인스턴스 제거 dropna(drop not a number)2. 비어있는 해당 특성을 삭제한다.
sample_incomplete_rows.drop("total_bedrooms", axis=1) # option 2, 해당 특성 제거, total_bedrooms 삭제3. 비어있는 값을 다른 값으로 대체한다(중간값, 평균 등등)
median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True) # option 3: 다른 값으로 채우기, 중간 값으로 채움
SimpleImputer 클래스로 대응하기
비어있는 값을 채우기 위한 sklearn에서 만든 SimpleImputer 클래스가 존재합니다.
● SimpleImputer는 여러 가지 전략을 통해 결측값을 대체할 수 있습니다
- 평균값(mean): 각 열의 평균값으로 결측값을 대체합니다. 수치형 데이터에 적합합니다.
- 중앙값(median): 각 열의 중앙값으로 결측값을 대체합니다. 수치형 데이터에 적합하며, 이상치(outliers)의 영향을 줄일 수 있습니다.
- 최빈값(most_frequent): 각 열의 최빈값으로 결측값을 대체합니다. 수치형 및 범주형 데이터 모두에 적합합니다.
- 상수값(constant): 사용자 정의 상수값으로 결측값을 대체합니다. 특정 값을 지정하여 결측값을 대체하고 싶을 때 사용합니다.
평균값: 1,2,3,4,5 = (1+2+3+4+5) / 5
중앙값: 1,2,3,4,5 = (1+5) / 2
● 집값을 예측하는 현재 데이터에서는 median을 사용하여 중간값으로 채웁니다.
from sklearn.impute import SimpleImputer #데이터셋에 비어있는 특성값을 채우기 위한 변환기
imputer = SimpleImputer(strategy="median") #클래스를 중간값 채우기로 설정
# (strategy="median"은 중간값으로 채운다는것을 의미한다)
● 중간값이 수치형 특성에서만 계산될 수 있기 때문에 텍스트 특성인 ocean_proximity를 제외한 데이터 복사본을 생성합니다. (중요)
housing_num = housing.drop("ocean_proximity", axis=1) # 숫자가 아닌 특성인 ocean_proximity 제거
# alternatively: housing_num = housing.select_dtypes(include=[np.number])
● 원본 데이터에서 housing에서 ocean_proximity 특성을 뺀 나머지 데이터에서 비어있는 값이 있으면 중간값으로 대체합니다.
- fit = 학습
# imputer 객체를 사용하여 housing_num 데이터프레임에서 중간값을 계산한다.
# fit()메서드를 호출하면 imputer객체가 housing_num 데이터프레임에서 각 열의 중간값 계산
imputer.fit(housing_num) # imputer클래스한테 housing_num 데이터의 중간값을 계산하고 비어있는 곳에 채우도록 학습
● 다음 명령어를 수행하면 채워질 각 특성들의 중간값을 확인할 수 있습니다.
- imputer는 각 특성의 중간값을 계산해서 그 결과를 객체의 statistics_ 속성에 저장합니다.
imputer.statistics_ # 중간값 확인 (채워질 값)
● SimpleInputer와 median 함수를 사용하여 결과를 비교하여 같은지 확인할 수도 있습니다.
# SimpleImputer와 직접 median()을 이용해 계산한 결과 비교
housing_num.median().values
학습된 imputer 객체를 사용해 훈련 세트에서 누락된 값을 학습한 중간값으로 바꿀 수 있습니다.
- fit(학습)된 imputer 객체로 housing_num에 비어있는 값을 transform(변환)시켜준다.
- imputer.fit_transform(housing_num)메서드로 훈련과 변환을 한번에 시킬 수 있다.
# housing_num에서 빠져있던 값들이 imputer에 설정된 중간값으로 채워진다.
X = imputer.transform(housing_num) # 빠져있던 것들이 채워진다.아래는 변형된 특성들이 들어 있는 평범한 numpy 배열이다. 이를 다시 pandas DataFrame으로 되돌린다.
# housing_tr: 새로운 데이터프레임을 저장할 변수
# pd.DataFrame() 생성자를 사용해 새로운 데이터프레임을 만든다
# X = 비어있던 값을 중간값으로 채워넣은 데이터(housing_num)가 들어간다.
# columns: 열 이름을 지정한다. housing_num의 열 이름과 동일하게 설정
# index=housing.index: housing(원본) 인덱스를 그대로 사용해 행 인덱스를 원본과 동일하게 설정
housing_tr = pd.DataFrame(X, columns=housing_num.columns, #훈련셋의 누락된 값을 중간값으로 채우기
index=housing.index) #NumPy 배열을 Pandas DataFrame으로 되돌리기
# 비어있던 특성의 행에 중간값들이 채워진게 보여진다.
housing_tr.loc[sample_incomplete_rows.index.values]
숫자가 아닌 값에 대응하기
추가로 숫자가 아닌 데이터를 처리해야하는 경우가 있을 수 있습니다. housing 데이터에서 범주형특성인 "ocean_proximity" 열 값을 housing_cat에 담습니다.
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
텍스트에서 숫자로 변환하기 (해결방법 X)
범주형 특성은 각 범주에 대응하는 숫자로 변환하되 숫자로만 표현하면 실제 값의 의미하고는 멀어질 수 있는 값이 배정될 수 있습니다.
그러므로 one-hot인코딩(이진특성)을 만들어서 해결할 수 있습니다. 이를 위해 sklearn의 OrdinalEncoder 클래스를 사용합니다.
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder() #각 범주를 대응하는 숫자로 변환
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]
# housing_cat: ocean_proximity의 값을 갖고
# fit_transform(): 학습과 변환을 한 번에 housing_cat을 이용하여 학습과 변환
값은 array([[0.], [0.], [4.], [1.], [0.], [1.], [0.], [1.], [0.], [0.]]) 입니다.
- 하지만 위처럼 값을 표현하면가까이 있는 두 값이 떨어져 있는 두 값보다 유사하다고 판단하는 문제가 발생합니다.
- 예를 들어 0과 4보다 0과 2가 더 가깝습니다 (숫자 상으로는), 그러나 실제로는 4( NEAR OCEAN)이 2(ISLAND)보다 0 (<1H OCEAN)과 유사합니다.
- 정수보다 이진 특성을 만들어서 해결할 수 있습니다 -> one-hot 인코딩
텍스트에서 숫자로 변환하기 (해결방법 O)
sklearn에서 제공하는 one-hot 인코딩을 사용한다면 범주의 값을 원-핫 벡터로 바꾸기 위한 OneHotEncoder 클래스를 제공합니다.
from sklearn.preprocessing import OneHotEncoder
# 두개의 백터의 값을 제곱해서 차를 더하고 제곱근을 씌워준다.
cat_encoder = OneHotEncoder()
# housing_cat = housing[["ocean_proximity"]] 범주형 특성이다.
# fit_transform(): 학습과 변환을 한 번에 housing_cat을 이용하여 학습과 변환
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hothousing_cat_1hot.toarray() # 범주형 특성을 가지고 핫인코딩한 결과
# 밀집 배열을 출력하도록 설정, True면 희소 행열을 출력
# cat_encoder 객체를 사용하여 범주형 데이터인 Housing_cat을 원-핫 인코딩한다.
cat_encoder = OneHotEncoder(sparse_output=False)
# fit_transform 메서드로 housing_cat 데이터프레임의 각 범주형 특성을 원-핫 인코딩하여 수치형 특성으로 변환
# 결과 데이터는 housing_cat_1hot에 저장, fit_transform으로 변환 작업 수행
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
변환기 함수로 만들기
추가로 나만의 변환기를 만들어서 새로운 특성을 만들 수 있습니다.
- init 으로 add_bedrooms_per_room을 True로 만든다면 add_bedrooms_per_room 특성을 생성하는 클래스입니다.
- rooms_per_household (방 수 / 인구수) 특성을 만듭니다
- population_per_household ((방 수 / 인구수) / 방 수) 특성을 만듭니다.
- 이후 새로 bedrooms_per_room 특성을 만들지 말지를 결정하고 새롭게 만든 특성들을 반환합니다
from sklearn.base import BaseEstimator, TransformerMixin
#사용자 정의 변환기를 정의하고 해당 변환기를 사용하여 데이터셋으로 새로운 특성을 만들기
# column index, 데이터셋의 열 인덱스를 나타내는 변수들, 특정 열을 접근할 때 사용
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
# 사용자 정의 변환기를 정의합니다. 이 클래스는 BaseEstimator, TransformerMixin 클래스를 상속받는다.
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
# add_bedrooms_per_room은 나중에 특성을 추가할 때 침실 수 대비 방의 비율을 추가할지 여부를 결정
def __init__(self, add_bedrooms_per_room=True): # no *args or **kargs
self.add_bedrooms_per_room = add_bedrooms_per_room
# 학습 데이터셋을 입력받아 아무 작업을 수행하지 않고 self를 반환
# 변환기는 아무런 학습을 하지 않기때문에 빈 메서드로 정의
def fit(self, X, y=None):
return self # nothing else to do
# 변환을 수행하는 메서드로, 주어진 데이터셋 X에 대해 새로운 특성을 계산하고 반환
def transform(self, X):
# 가구당 방의 수를 계산한다
# X에서 rooms_ix에 해당하는 열과 Households_ix에 해당하는 열의 값을 나눈다.
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
# 가구당 인구 수를 계산한다. 인구수 / 가구수
# X에서 population_ix에 해당 열과 households_ix에 해당 열의 값을 나눈다.
population_per_household = X[:, population_ix] / X[:, households_ix]
# 매개변수가 True인 경우 침실 수 대비 방의 비율을 계산
if self.add_bedrooms_per_room: #
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
# return np.c_[인자값, 가구당 방의 수, 가구당 인구 수, 방당 침대 수]
# np.c_: 두 개의 1차원 배열을 칼럼으로 세로로 붙여서 2차원 배열 만들기
return np.c_[X, rooms_per_household, population_per_household,
bedrooms_per_room]
else: # 침실 수 대비 방의 비율을 추가하지 않는다.
# np.c_: 두 개의 1차원 배열을 칼럼으로 세로로 붙여서 2차원 배열 만들기
return np.c_[X, rooms_per_household, population_per_household]
# CombinedAttributesAdder클래스의 attr_adder 객체를 만든다.
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
# 위에서 만든 변환기로 housing의 값들로 X(housing.values), rooms_per_household,
# population_per_household 값들을 2차원 배열로 반환한다.
housing_extra_attribs = attr_adder.transform(housing.values)
특성 스케일링
- 데이터에 적용할 가장 중요한 변환 중 하나가 특성 스케일링입니다. 입력 숫자 특성들의 스케일이 많이 다르면 잘 동작하지 않습니다.
- 즉, 전체 방 개수의 범위는 6에서 39,320인 반면에 중간 소득의 범위는 0에서 15까지인 경우가 예시로 들 수 있겠습니다.
- 스케일링을 하는 방법은 min-max 스케일링(정규화)이 가장 간단합니다, sklearn에서는 MinMaxScaler 변환기를 제공한다.
-> 0~1 범위에 들도록 값을 이동하고 스케일을 조정하면 된다, 데이터에서 최솟값을 뺀 후 최대값과 최솟값의 차이를 나누면 이렇게. 할 수 있다. - 하지만 표준화는 다릅니다. 먼저 평균을 뺀 후 표준편차로 나눠 결과 분포의 분산이 1이 되도록 합니다.
-> sklearn에서 StandardScaler 변환기 제공
변환 파이프라인
앞에 있었던 내용들을 순서대로 실행해야합니다.
- sklearn에는 연속된 변환을 순서대로 처리할 수 있도록 도와주는 Pipeline 클래스가 있습니다.
- Pipline 클래스를 이용하면 여러 작업을 Pipline 으로 설정하여 마지막에 fit_transform 메서드로 차례로 작업을 진행합니다.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# StandardScaler: 분산 1을 갖도록 변환하는 표준화 스케일링 함수
# 이 객체는 여러 단계의 데이터 전처리를 연속적으로 적용할 수 있도록 도와주며 이름과 해당 단계를 지정한다.
num_pipeline = Pipeline([
# 빈 값을 대체할 값을 중간값으로 설정한다.
('imputer', SimpleImputer(strategy="median")), #imputer.fit(데이터값)해야함
# 새로운 특성을 추가하는 작업을 수행 하지만 여기서는 추가안하는듯, 이 작업을 attribs_adder라는 이름으로 지정
('attribs_adder', CombinedAttributesAdder()),
# 데이터의 표준화를 수행하는 작업을 수행한다. std_scaler라는 이름으로 작업 이름 지정하고 StandardScaler 객체를 사용
('std_scaler', StandardScaler()),
])
# 파이프라인을 훈련 데이터셋인 housing_num(범주형특성을 제외한 계층적샘플링을 통해 선별한 값)에 적용
# 즉 위에서 3가지 작업을 연속으로 지정할 전처리를 housing_num을 대상으로 하여
# 작업이 끝난 값을 housing_num_tr에 넣는다.
# fit_transform: 데이터를 학습하고 주어진 데이터를 변환하는 것이다.
housing_num_tr = num_pipeline.fit_transform(housing_num)# num_pipeline를 활용한다.
# 1.비어있는 값을 중간값으로 설정한다.
# 2.새로운 특성을 추가한다. (rooms_per_household, population_per_household)
# 3.표준화 알고리즘으로 데이터를 스케일링한다.
housing_num_tr
이제 full_pipeline을 만듭니다. 위에서 만들어준 Pipline과 OneHotEncoding을 동시에 작업할 수 있도록 sklearn에서 제공하는 ColumnTransformer가 추가되었습니다.
- ColumnTransformer를 사용하여 fit_transform 를 해줌으로 파이프라인을 훈련시킴과 동시에 housing 데이터를 변환할 수 있다.
from sklearn.compose import ColumnTransformer
#scikit-learn 라이브러리에서 ColumnTransformer 클래스를 가져온다
#ColumnTransformer는 데이터프레임의 열에 대한 다양한 전처리 단계를 쉽게 적용할 수 있도록 도와주는 도구다
#list는 데이터프레임 또는 배열의 모든 열을 리스트 형태로 변환한다.
#ocean_procimity 값이 빠진 수치형 특성의 열 이름을 저장
num_attribs = list(housing_num)
#범주형 특성인 ocean_proximity 열에 대해 OneHotEncoder를 사용하여 원핫 인코딩 수행
cat_attribs = ["ocean_proximity"]
#특성의 열에 따라 맞는 처리를 위해(즉, 숫자 변환, 텍스트/범주 변환)
#ColumnTransformer 클래스 활용
full_pipeline = ColumnTransformer([
# 위에서 만든 num_pipline을 사용하여 num_attribs에 포함된 숫자형 특성들을 전처리한다.
("num", num_pipeline, num_attribs),
# OneHotEncoder를 사용하여 ocean_proximity 열을 원-핫인코딩한다.
("cat", OneHotEncoder(), cat_attribs),
])
#원본 데이터프레임을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터를 Housing_prepared에 넣는다.
housing_prepared = full_pipeline.fit_transform(housing)
모델 훈련
위에 과정을 통해 따라오면 이제 모델을 사용하여 데이터 훈련시킬 수 있습니다.
1. 먼저 선형 회귀 모델 알고리즘인 LinearRegression()를 사용하여 전처리가 끝난 데이터와 정답을 가지고 모델을 생성 및 학습시킵니다
from sklearn.linear_model import LinearRegression
#선형 회귀 모델을 생성한다.
lin_reg = LinearRegression()
#housing_prepared: 원본 데이터프레임을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터를 Housing_prepared에 넣는다.
#housing_labels: 계층적샘플링을 통해서 얻은 실제집값
#선형 회귀 알고리즘으로 학습시킨다.
# fit은 훈련 -> 모델 파라미터를 찾아낸다.
# housing_prepared: 전처리가 끝난 데이터, housing_labels: 레이블(정답,실제 집값)데이터
lin_reg.fit(housing_prepared, housing_labels)
#값을 예측하는 모델을 만든 것이다.
2. 선형 회귀 알고리즘으로 훈련된 모델을 사용해 값을 예측해봅니다
- 원본 데이터 프레임에서 5개의 값만 뽑아서 값을 예측하는 것입니다.
# let's try the full preprocessing pipeline on a few training instances
# 전체 데이터셋에서 5개 인스턴스를 가지고 학습한 모델에 적용하여 결과값 예측
#some_data: 원본 데이터프레임에서 처음 5개의 데이터 행을 선택하여 저장한다.
some_data = housing.iloc[:5]
#some_labels: 학습 데이터에 대한 실제 타겟값을 나타내는 housing_labels에서 처음 5개의 레이블을 선택하여 저장
#some_labels는 모델이 예측한 결과와 비교하기 위한 실제값이다.
#계층적샘플링을한 것
some_labels = housing_labels.iloc[:5]
#전처리 파이프라인을 사용하여 some_data에 대한 전처리를 수행하고 전처리된 데이터를 저장한다.
some_data_prepared = full_pipeline.transform(some_data)
#선형 회귀 알고리즘을 사용하여 fit(훈련)된 lin_reg 모델을 사용하여 predict(예측)을 수행
#lin_reg 모델을 사용하여 some_data_prepared에 대한 예측을 수행하고 예측값을 출력한다.
print("Predictions:", lin_reg.predict(some_data_prepared))#실제 집값으로 전처리 파이프라인을 사용해 전처리한 데이터를 가지고 선형회귀 모델로 예측한 값과
#아래에 비교하기 위한 실제 집값을 의미한다.
print("Labels:", list(some_labels))
지금까지 한 작업들을 간략하게 정리하면
-> 중위소득이 집값을 예측하는데 매우 중요하다고 해서 중위소득(정답 레이블)을 제외한 특징들을 가공(전처리)한다
-> 가공된 특징 데이터들을 가지고 머신러닝 알고리즘 모델을 만들어 모델을 학습시킨다.
-> 중위소득을 기반으로 집값을 예측하는 모델을 만들었으면 그 모델에 값을 넣어서 테스트셋 값을 예측해보라고 시킨다.
-> 중위소득을 기반으로 집값을 예측하도록 훈련된 모델이 테스트셋 값으로 예측한 집값을 출력한다.
하지만 첫 번째 문장을 보면 중위 소득이 집값을 예측하는데 매우 중요하다고 해서 중위 소득을 기반으로 데이터를 가공해서 모델을 훈련시켰지만 만약에 중위 소득이 아니라 다른 특성이 더 집값하고 긴밀한 관계가 있다고 하면 문제가 발생합니다.
- 그래서 피어슨의 r 을 사용해서 상관관계를 파악하는 것입니다.
- 만약 새로운 특성을 만들었는데 해당 특성이 중위 소득보다 더 상관관계가 깊다면? 그 특성을 기반으로 다시 데이터를 가공하고 모델을 훈련시킨 후 훈련된 모델로 값을 예측하면 됩니다.
모델의 측정값 RMSE로 평가
모델을 훈련하고 훈련된 모델로 집값을 예측해봤으면 이제 그 값이 얼마나 정확한지, 오류가 어느정도 있는지를 확인해야힙니다.
- 그러기 위해서는 평균 오차 제곱근을 구해서 평균적인 오차 범위를 구할 수 있습니다.
- full_pipeline 을 통해서 가공이 끝난 원본 데이터(housing_prepared)로 값을 예측해서 housing_predictions 에 값을 넣습니다.
- 계층적샘플링으로 나눈 집값(즉 정답 레이블)과 housing_predictions(예측한 값)을 가지고 평균 오차 제곱을 구합니다.
- 평균 오차 제곱을 구한 값에 제곱근(sqrt)를 씌워서 RMSE 로 변환합니다 -> RMSE 의 값은 68633.40810776998 이 나옵니다.
RMSE: 회귀(regression) 문제에서 사용하는 전형적인 성능 지표
from sklearn.metrics import mean_squared_error
#mean_squared_error로 평균 오차 제곱을 구하고
#sqrt를 하여 평균 오차 제곱 근을 구해 평균적인 오차 범위를 알 수 있다.
#housing_prepared는 원본 데이터프레임(housing)을 가지고 모든 전처리 단계를 거쳐서 가공된 데이터
#lin_reg 선형회귀 모델을 사용하여 학습 데이터에 대한 예측을 수행하고, 이 예측값을
#housing_predictions에 저장한다. 즉, 모델이 학습 데이터에 대한 주택 가격 예측을 수행한 결과
#array([[-0.94135046, 1.34743822, 0.02756357, ..., 0. ,0. , 0. ] 이런 값들을 가지고 계산해준다.
housing_predictions = lin_reg.predict(housing_prepared)
#housing_labels: 계층적샘플링으로 나눈 집값
#housing_predictions: 원본 데이터를 선형회귀 모델로 값을 구한 집값
#함수를 사용하여 예측값과 실제값 사이의 평균 제곱 오차를 계산한다.
#lin_mse는 예측 오차의 제곱을 모든 데이터 포인트에 대해 평균한 값
lin_mse = mean_squared_error(housing_labels, housing_predictions) # 둘이 순서 바꿔도 똑같다
#계산된 mse값을 제곱근을 씌워서 RMSE로 변환
lin_rmse = np.sqrt(lin_mse)
#실제 중간 주택 가격과 약 $68633 오차가 있다는 것을 의미한다. 줄일수록 좋은것
lin_rmse #
위에서는 오차범위가 68633이나 되며 이를 해결하기 위해서는 더욱 강력한 모델을 사용하는 방법이 있습니다.
아래는 결정 트리 회귀 모델을 사용한 것이고 훈련 방법은 선형 회귀하고 똑같습니다.
- 값이 매번 랜덤하지 않도록 seed값을 42로 설정합니다.
- full_pipeline 을 거쳐서 가공(전처리)된 housing_prepared 데이터로 계층적샘플링으로 구한 housing_labels(실제 집값)을 맞추도록 학습시킵니다.
from sklearn.tree import DecisionTreeRegressor
#선형회귀모델은 약해서 언더피팅 모델이다.
#그러기 위해서 더 강력한 모델인 결정 트리 회귀 모델을 사용하는 것이다.
tree_reg = DecisionTreeRegressor(random_state=42)
# housing_prepared: 전처리가된 원본 데이터
# 계층적 샘플링으로 나눈 집값 (답안지라고 부르심)
tree_reg.fit(housing_prepared, housing_labels)
# 값을 예측하기 위한 모델 만들기, 모델.fit(x(i)값, y(i)값)
위에서 훈련된 데이터로 값을 예측한 값으로 평균 오차 제곱근을 구하면 값이 0이라는 값이 나오는데 이는 의심해봐야하는 상황입니다.
#housing_prepared: 전처리된 원본 데이터
housing_predictions = tree_reg.predict(housing_prepared)
# h(x) = housing_labels, y=housing_predictions
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
교차검증
교차 검증을 통해서 학습 모델을 평가할 수 있습니다.
교차 검증이란?
- 훈련셋을 k-폴드로 나눕니다
- k-1 폴드를 이용해서 ML 모델을 훈련하고 나머지 폴드를 이용해 모델 성능을 검증합니다
- 위 과정을 k번 반복하여 최적의 파라미터 (모델, 하이퍼파라미터)를 찾아 모델 확정합니다
- sklearn에서 k-폴드 교차 검증 CV 함수인 cross_val_score 를 제공하고 있습니다.

모델마다 다른 결과
추가로 아래를 확인했을 때와 같이 모델도 종류마다 성능이 다릅니다.
#lin_reg: 선형회귀 모델을 사용해서 얻은 결과값
#housing_prepared는 전처리된 주택 데이터의 특성들, 교차 검증에 사용할 데이터셋
#housing_labels는 계층적샘플링을 통해서 얻은 집값들로 답안지
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)

아래는 결정회귀 회귀 모델을 사용한 코드입니다.
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
tree_reg = make_pipeline(preprocessing, DecisionTreeRegressor(random_state=42))
tree_reg.fit(housing, housing_labels)
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
#tree_rmse_scores = np.sqrt(-scores): 교차 검증에서 계산된 음수 MSE를 다시 양수로 변환하고 루트를 씌워 제곱근 RMSE값을 계산한다.
tree_rmse_scores = np.sqrt(-scores)
앞에 선형회귀 모델을 사용했을떄 RSME가 $2,731 이였지만, 교차 검증을 통해서 확인해본 결과 평균오차가 $71,407, 표준편차가 $2,439라는 것을 확인할 수 있습니다.
#교차검증을 통해서 얻은 결과값
def display_scores(scores):
print("Scores:", scores) # 점수
print("Mean:", scores.mean()) # 평균
print("Standard deviation:", scores.std()) # 표준편차
display_scores(tree_rmse_scores)
'AI > Machine Learning' 카테고리의 다른 글
| 사이킷런 scikit-learn 이란? (0) | 2024.07.09 |
|---|---|
| 여러 개의 레이블을 갖는 하나의 데이터 분류하기 - 다중 레이블 분류 (2) | 2024.07.08 |
| 머신러닝 분류 (숫자 예측) (0) | 2024.07.07 |
| 머신러닝 모델 튜닝하기 (0) | 2024.06.28 |
| 머신러닝 시작하기 (0) | 2024.06.26 |
